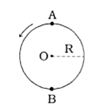
\(A\) મણકો નીચે ઊતરીને સાથે અથડામણ અનુભવે ત્યારે
\(\frac{1}{2}{m_1}{\upsilon _1}^2\,\, = \,\,{m_1}g(2R)\,\,\) (સ્થિતિઉર્જા નું ગતિઉર્જા માં રૂપાંતર)
\(\therefore {\upsilon _1}^2 = 4gR\,\,\,\,\therefore \,\,\,{\upsilon _1}\, = \,\sqrt {4gR} \,\,\,\,...\,\,...\,\,...\,\,(1)\)
હવે, \(A\) અને \(B \) ની અથડામણ સ્થિતિસ્થાપક હોવાથી , વેગમાં સરક્ષણ નિયમ અનુસાર \(, m_1u_1 = m_2u_2\)
\(\therefore \,{\upsilon _2}\, = \,\frac{{{m_1}}}{{{m_2}}}\,\sqrt {4gR} \,\,\,\,...\,\,...\,\,\,...\,(2)\)
હવે, અથડામણ બાદ \(B \) મણકો કેન્દ્ર \(O\) ની ઊંચાઈ એ એટ્લે \(R \) જેટલી ઊચાઇએ પહોચે છે.
\(\frac{1}{2}{m_2}{\upsilon _2}^2\,\, = \,{m_2}gR\) ( ગતિઉર્જા નું સ્થિતિઉર્જા રૂપાંતર)
\(\therefore \,{\upsilon _2}^2\, = \,\,2gR\,\,\,\,\therefore \,\,\,{\upsilon _2}\,\, = \,\,\sqrt {2gR} \)
\({\upsilon _{\text{2}}}\) ની કીમત સમીકરણ (2) માં મુક્તા \(,{\text{ }}\sqrt {2gR} \, = \,\frac{{{m_1}}}{{{m_2}}}\sqrt {4gR} \,\,\,\therefore \,\,\,\frac{{{m_1}}}{{{m_2}}}\,\, = \,\frac{{\sqrt {2gR} }}{{\sqrt {4gR} }}\,\, = \,\,\frac{1}{{\sqrt 2 }}\)
Download our appand get started for free
Similar Questions
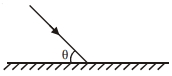
- 1$u$ ઝડપ સાથે ગતિ કરતો .... દળનો દડોએ આકૃતિમાં દર્શાવ્યા મુજબ લીસી સમક્ષિતિજ સપાટી સાથે $\theta$ ખૂણે અથડામણ અનુભવે છે. દડા વડે સપાટી પર લાગતા આઘાતની માત્રા કેટલી છે. અથડામણનો રેસ્ટીટ્યુશન અંક $e$ છે]View Solution
- 2$M$ દળ એ $m$ દળ કરતાં ઘણો વધારે છે. $M$ દળનો ભારે પદાર્થ $v$ વેગથી સ્થિર $m$ દળના હલકા પદાર્થ સાથે સંપૂર્ણ સ્થિતિસ્થાપક સંઘાત અનુભવે છે. તો અથડામણ પછી હલકા પદાર્થનો વેગ કેટલો થશે?View Solution
- 3કોલમ $-I$ અને કોલમ $-II$ સાથે જોડો.View Solution
કોલમ $-I$ કોલમ $-II$ $(1)$ સંરક્ષી બળ $(a)$ ઘર્ષણ બળ $(2)$ અસંરક્ષી બળ $(b)$ ગુરુત્વાકર્ષણ બળ $(c)$ આંતરિક બળ - 4લીફ્ટમાં $60\; HP$ ક્ષમતા ધરાવતી ઇલેક્ટ્રિક મોટર મહત્તમ $2000\; \mathrm{kg}$ ઉચકાવી શકે છે. જો લીફ્ટમાં ઘર્ષણબળ $4000 \;\mathrm{N}$ હોય તો મહત્તમ ક્ષમતાથી ભરેલ લિફ્ટ કેટલા ............. $\mathrm{m} / \mathrm{s}$ ના વેગથી ગતિ કરી શકે?View Solution
$\left(1 \;\mathrm{HP}=746 \;\mathrm{W}, \mathrm{g}=10\; \mathrm{ms}^{-2}\right)$
- 5$3.7\, kg.wt$ તણાવ સહન કરી શકતી દોરી પર $500 \,gm$ નો પદાર્થ બાંધીને $4\,m$ ત્રિજયાના શિરોલંબ સમતલમાં વર્તુળમય ગતિ કરાવવામાં આવે છે.તો તેની મહત્તમ કોણીય ઝડપ ........ $rad/\sec$ થાય.View Solution
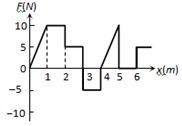
- 6બળ $F$ અને અંતર $ x$ વચ્ચેનો સંબંધ આકૃતિમાં દર્શાવ્યા પ્રમાણે છે તો પદાર્થ દ્વારા $x = 1 m$ થી $x = 5 m$ સ્થાંનાતર થવા માટે કરવું પડતું કાર્ય =….$J$View Solution
- 7$m$ દળ એક બ્લોક ને $\frac{g}{3}$ અચળ પ્રવેગે શિરોલંબ રીતે ઉપર તરફ $h$ અંતર જેટલું ખેંચવા માટે એક દોરીના ઉપયોગ કરવામાં આવે છે. દોરીમાંના તણાવ વડે થયેલ કાર્ય છે...View Solution
- 8પાણીનો પંપ $100 kg$ ના પાણીને $5 sec$ માં $10m$ ઊંચાઇ પર લઇ જાય છે.જો પંપની કાર્યક્ષમતા $60\%$ હોય,તો પંપનો પાવર કેટલા .............. $\mathrm{kW}$ હશે?View Solution
- 9$200\,g$ નો એક બોલ $20\,m$ ઊંચા થાંભલા ઉપર સ્થિર સ્થિતિમાં છે.$10\,g$ ની અને $u\,m/s$ ના વેગથી સમક્ષિતિજ દિશામાં ગતિ કરતી એક ગોળી (બુલેટ) બોલના કેન્દ્રને અથડાય છે સંઘાત બાદ બંને એકબીજાથી સ્વતંત્ર રીતે ગતિ કરે છે.બોલ જમીન ઉપર થાંભલાના તળિયે થી $30\,m$ અંતરે અને બુલેટ $120\,m$ અંતરે પડે છે. બુલેટનો વેગ $..............m/s$ હશે.($\left.g =10 m / s ^2\right.$ છે.)View Solution
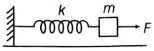
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે ઘર્ષણરહિત સપાટી પર રહેલ $m$ દળના બ્લોકને $k$ જેટલા બળઅચળાંક ધરાવતી સ્પ્રિંગ સાથે બધીને દીવાલ સાથે જોડેલ છે. શરૂઆતમાં તે મૂળભૂત અવસ્થામાં છે. જો તેના પર જમણી બાજુ $F$ જેટલું અચળ બળ લગાવતા સ્પ્રિંગ $x$ જેટલી ખેંચાઇ ત્યારે બ્લોકનો વેગ કેટલો હશે?View Solution