we will find the relation for small temperature changes.
resistance \(R =\rho L / A\)
coefficient of linear expansion \(= \alpha\)
length of conductor: \(L = L _0(1+ a \Delta T ) \quad \Delta L = a L _0 \Delta T\)
\(\beta=\) coefficient of expansion in area : \(=2 \alpha\)
Area of cross section: \(A=A_0(1+2 \alpha \Delta T)\)
\(\Delta A=2 \alpha A_0 \Delta T\)
Resistivity \(\rho=\rho_0(1+\alpha_p \Delta T)\)
\(\Delta \rho=\rho_0 \alpha_p \Delta T\)
Resistance \(R = R _0(1+\alpha_R \Delta T )\)
\(\Delta R =\alpha_R R _0 \Delta T\)
If \(\Delta A =2 a \Delta T\) is very small then, and for small \(\Delta T\),
\(R_0=\rho_0 L_0 / A_0\)
\(R =\rho_0(1+ \alpha_p \Delta T ) L _0(1+ a \Delta T ) /\left[ A _0(1+2 \alpha \Delta T )\right]\)
\(=\left(\rho_0 L_0 / A_0\right)(1+\alpha_p \Delta T)(1+\alpha \Delta T)(1-2 \alpha \Delta T)\)
\(=R_0(1+\alpha_p \Delta T)(1-a \Delta T) \quad\) ignoring the \(2 a^2 \Delta T^2\) term
\(=R_0[1+(\alpha_p-\alpha) \Delta T] \quad\) ignoring the \(A \rho a \Delta T^2\) term
\(\alpha_R=\alpha_P-\alpha\)
Download our appand get started for free
Similar Questions
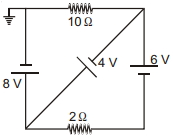
- 1આકૃતિમાં દર્શાવેલ પરિપથમાં બધા જ કોષો આદર્શ છે. $2\; \Omega$ અવરોધમાંથી પસાર થતો વિદ્યુતપ્રવાહ $............A$ છે.View Solution
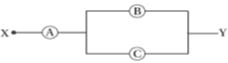
- 2આકૃતિમાં દર્શાવ્યા અનુસાર $R,\,1.5 R $ અને $3R $ અવરોધના અનુક્રમે $ A,\,B$ અને $C$ વોલ્ટમીટર જોડેલા છે.જયારે $X$ અને $ Y$ વચ્ચે અમુક વિદ્યુતસ્થિતિમાનનો તફાવત લાગુ પાડતા અનુક્રમે વોલ્ટમીટર $A,\,B $ અને $C$ ના અવલોકનો $V_A,\,V_B$ અને $V_C$ મળે તો _________View Solution
- 3જો વિદ્યુત પ્રવાહમાં $20 \%$ ઘટાડો કરવામાં આવે તો બલ્બના પ્રકાશની તીવ્રતામાં કેટલા ટકા ધટાડો થાય?View Solution
- 4$300\,K$ તાપમાને રહેલા એક સિલિકોનના ચોસલાની લંબાઈ $10\ cm$ અને આડછેદનું ક્ષેત્રફળ $1 \times 10^{-4}\ m^2$ છે. જો તેના બે છેડા વચ્ચે $2\ V$ ની બેટરી લંબાઈને સમાંતર જોડવામાં આવે તો તેમાંથી પસાર થતો પ્રવાહ શોધો. ઈલેક્ટ્રોનની મોબિલિટી $0.14\, m^2V^{-1}S^{-1}$ તથા ઈલેક્ટ્રોન સંખ્યા ઘનતા $1.5 \times 10^{16}\, m^{-3}$ છે.View Solution
- 5આપેલ પરિપથમાં બધા અવરોધ $R$ ના છે. $A$ અને $B$ ટર્મિનલ વચ્ચેનો સમતુલ્ય અવરોધ કેટલો થાય?View Solution
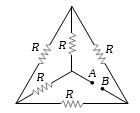
- 6એક વાહક તારમાંથી પ્રતિ સેકન્ડે $10^{7}$ ઇલેક્ટ્રોન વહન પામતા હોય તો તારનો પ્રવાહ કેટલો હશે?View Solution
- 7આપેલ પોટેન્શિયોમીટર માં $400\, cm$ લંબાઈના તારનો ઉપયોગ થયો છે.તારનો અવરોધ $r = 0.01\, \Omega /cm$ છે.જ્યારે એક જૉકીને આકૃતિમાં દર્શાવ્યા પ્રમાણે $A$ બિંદુથી $50\, cm$ દૂર રહેલ $J$ બિંદુ પર લઈ જવામાં આવે ત્યારે જૉકી સાથે જોડેલ વોલ્ટમીટર કેટલા ................ $V$ આવર્તન દર્શાવશે?View Solution
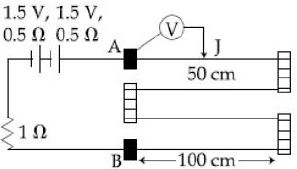
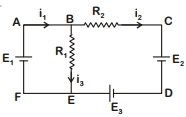
- 8આપેલ પરિપથ માટે લૂપ $BCDEB$ માટે કિચોર્ફનો નિયમ લગાવતા સમીકરણ .............. મુજબ મળેView Solution
- 9$10\,\Omega$ નો એક એવા $10$ અવરોધને મહત્તમ અને ન્યૂનત્તમ સમતુલ્ય અવરોધ મળે તે રીતે જોડવામાં આવે છે. મહત્તમ અને ન્યૂનતમ સમતુલ્ય અવરોધનો ગુણોત્તર ...... થશે.View Solution
- 10તાંબામાં મુક્ત ઇલેકટ્રોનની સંખ્યા ઘનતા લગભગ $8 \times 10^{28}\,m ^{-3}$ જેટલી છે. તાંબાના તારના આડછેદનું ક્ષેત્રફળ $= 2 10^{-6}\,m ^2$ છે અને તે $3.2\,A$ પ્રવાહનું વહન કરે છે. ઇલેકટ્રોનની ડ્રીફટ ઝડપ $.......\times 10^{-6}\,ms ^{-1}$ છે.View Solution
