Initial momentum of the system block \((C)\)
\( = m{v_0}\) .After striking with \(A\), the block \(C\) comes to rest and now both block \(A\) and \(B\) moves with velocity \(v\) when compression in spring is \({x_0}.\)
By the law of conseravtion of linear momentum
\(m{v_0} = \left( {m + 2m} \right)v \Rightarrow \frac{{{v_0}}}{3}\)
By the law of conservation of energy
\(K.E. \,of\, block \,C = K.E.\ of\, system + P.E. of system\)
\(\begin{array}{l}
\frac{1}{2}mv_0^2 = \frac{1}{2}\left( {3m} \right){\left( {\frac{{{v_0}}}{3}} \right)^2} + \frac{1}{2}kx_0^2\\
\Rightarrow \,\frac{1}{2}mv_0^2 = \frac{1}{6}mv_0^2 + \frac{1}{2}kx_0^2\\
\Rightarrow \,\frac{1}{2}kx_0^2 = \frac{1}{2}mv_0^2 - \frac{1}{6}mv_0^2 = \frac{{mv_0^2}}{3}\\
\therefore \,\,\,\,\,\,\,k = \frac{2}{3}m{\left( {\frac{{{v_0}}}{{{x_0}}}} \right)^2}
\end{array}\)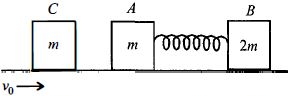
Download our appand get started for free
Similar Questions
- 1$x$-અક્ષ પર ગતિ કરી રહેલ એક કણની ( $t)$ સમયે સ્થિતિ $x$ એ $t=\sqrt{x}+2$ સમીકરણ વડે આપેલ છે જ્યાં $x$ મીટરમાં છે અને $t$ સેકન્ડમાં છે. બળ વડે પહેલી ચાર સેકન્ડો માં થયેલ કાર્ય ......... $J$View Solution
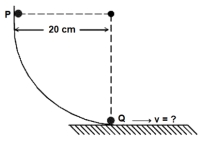
- 2આપેલ આકૃતિ મુજબ, એક નાનો બોલ $P$ વર્તુળના ચોથાભાગ પર સરકીને તેના જેટલું જ સાલ ધરાવતા બીજા બોલ $Q$ને અથડાય છે, કે જે પ્રારંભમાં વિરામ સ્થિતિમાં છે. ઘર્ષણની અસર અવગણતા અને સંઘાત સ્થિતિસ્થાપક છે તેમ ધારતા, $Q$ બોલનો સંઘાતબાદ વેગ $..........$ હશે. $\left( g =10\,m / s ^2\right)$View Solution
- 3$5\; kg$ દળના પદાર્થનું વેગમાન $10\; kg-m/s$ છે.તેના પર $0.2\; N $ બળ $ 10 \;seconds $ સમય સુધી લાગતાં ગતિઊર્જામાં થતો વધારો.....$J$View Solution
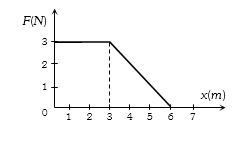
- 4એક પદાર્થ પર લાગતું બળ $F$, તેના સ્થાનાંતર $x$ સાથે આકૃતિમાં દર્શાવ્યા મુજબ બદલાય છે. બળ ન્યુટનમાં અને $x$ મીટરમાં છે. $x=0$ થી $x = 6\; m$ સુધી પદાર્થની ગતિ માટે બળ દ્વારા કેટલું કાર્ય ($J$ માં) થયું હશે?View Solution
- 5એક બોલ $ 'h'$ ઉંચાઈ પરથી મુક્ત રીતે પતન કરે છે. આ બોલ સતત પટકાઈને પાછો ફરે છે. પાછો ફરતો બોલ અટક્યા પહેલાં તેણે કેટલું અંતર કાપ્યું હશે?View Solution
- 6$V$ વેગથી જતી $m$ દળની ગોળી રેતી ભરેલ $M$ દળની થેલીમાં ધૂસીને સ્થિર થઇ જાય છે.જો થેલી $h$ ઊંચાઇ પર જતી હોય,તો ગોળીનો શરૂઆતનો વેગ કેટલો થાય?View Solution
- 7નીચે બે કથનો આપેલા છે.View Solution
કથન $I$ : સમાન ગતિ ઊર્જા વડે ગતિ કરતા ટ્રક અને કારને સમાન પ્રતિબળ ઉત્પન્ન કરતી બ્રેક લગાડીને ઉભા રાખવામાં આવે છે. બંને સમાન અંતર બાદ સ્થિર થશે.
કથન $II$: પૂર્વ દિશામાં ગતિ કરતી કાર વળીને ઉત્તર તરફ ગતિ કરે છે, તેની ઝડપ બદલાયા સિવાયની રહે છે. કારનો પ્રવેગ શૂન્ય છે.
ઉપર્યુક્ત કથનોના સંદર્ભમાં, નીચે આપેલ વિકલ્પમાંથી સાચો ઉત્તર પસંદ કરો.
- 8એક સ્થિર કણ $m_1$ અને $m_2$ દળવાળા બે કણોમાં વિસ્ફોટ પામીને તે વિરુદ્વ દિશામાં $v_1$ અને $v_2$ જેટલા વેગથી ગતિ કરે છે. તેમની ગતિઊર્જાનો ગુણોત્તર ${E_1}/{E_2}$ કેટલો થાય?View Solution
- 9સ્થિર સ્થિતિમાં રહેલા $m$ દળના પદાર્થ પર બળ લાગતાં $t_1$ સમયમાં $v_1$ વેગ પ્રાપ્ત કરે છે.તો $t$ સમય પછી પાવર કેટલો થાય?View Solution
- 10$10\,kg$ દળનો એક બ્લોક $x$-અક્ષ પર $F=5 x\,N$ બળની અસર હેઠળ છે. આ બળ વડે બ્લોકને $x=2\,m$ થી $4\,m$ સુધી ગતિ કરવા માટે કરવું પડતું કાર્ય ...... $J$ હશે.View Solution
