\( - ms\frac{{dT}}{{dt}} = e\sigma A\left( {{T^4} - T_0^4} \right)\)
\( - \frac{{dT}}{{dt}} = \frac{{e\sigma A}}{{ms}}\left( {{T^4} - T_0^4} \right)\,\,;\,\, - \frac{{dT}}{{dt}} = \frac{{4e\sigma AT_0^3}}{{ms}}\left( {\Delta T} \right)\)
\(T = {T_0} + \left( {{T_i} - {T_0}} \right){e^{ - kt}}\)
\(where\,k = \frac{{4e\sigma AT_0^3}}{{ms}}\)
\(k = \frac{{4e\sigma AT_0^3}}{{\rho vs}}\,\,;\,\,\left| {\frac{{dT}}{{dt}}} \right| \propto k\)
\(\therefore \left| {\frac{{dT}}{{dt}}} \right| \propto \frac{1}{{\rho s}}\)
\(\rho A{S_A} = 2000 \times 8 \times {10^2} = 16 \times {10^5}\)
\({\rho _B}{S_B} = 4000 \times {10^3} = 4 \times {10^6}\)
\({\rho _A}{S_A} < {\rho _B}{S_B}\)
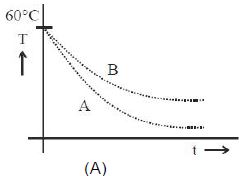
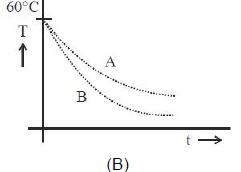
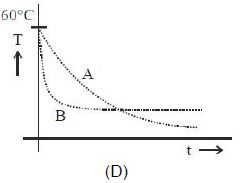
\({\left| {\frac{{dT}}{{dt}}} \right|_A} > {\left| {\frac{{dT}}{{dt}}} \right|_B}\)
Download our appand get started for free
Similar Questions
- 1જો પદાર્થનું તાપમાન $50\%$ વધારવામાં આવે,તો તેની ઉત્સર્જન ઊર્જામાં થતો $\%$ વધારો ...... $\%$ હશે?View Solution
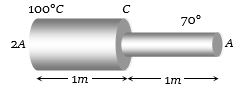
- 2સમાન દ્રવ્યમાંથી બનાવેલ સળિયા નીચે દર્શાવેલ છે .તો $C$ બિંદુનું તાપમાન ..... $^oC$ હશે ?View Solution
- 3એક નળાકાર ધાતુનો સળિયો જેના બે છેડા બે ઉષ્મા સ્થાનો સાથે ઉષ્મિય સંપર્કમાં રાખતા તેમાંથી $t$ સમયમાં $Q$ ઉષ્મા પસાર થાય છે. આ સળિયાને પિગાળીને તેમાંથી મૂળ સળિયા કરતાં અડધી ત્રિજયાનો નવો સળિયો બનાવવામાં આવે છે. જ્યારે આ નવા સળિયાના છેડાને બે ઉષ્મા સ્થાનો સાથે ઉષ્મિય સંપર્કમાં રાખવામાં આવે, તો આ નવા સળિયા દ્વારા $t$ સમયમાં પસાર થતી ઉષ્મા કેટલી હશે?View Solution
- 4બે પદાર્થ $A$ અને $B$ જેનું વજન, ક્ષેત્રફળ અને બાહ્ય સપાટી એક સરખાં છે જેની વિશિષ્ટ ઉષ્મા $S_A$ અને $S_B\left(S_A > S_B\right)$ છે તેમને આપેલા તાપમાને ઠંડા પાડવામાં આવે છે તો સમય સાથે તાપમાનમાં કેટલો ફેરફાર થાય?View Solution
- 5ત્રણ કાળો,ભૂખરો અને સફેદ પદાર્થ $2800\,^oC$ જેટલું તાપમાન સહન કરી શકે છે. ત્રણેય પદાર્થને ફર્નેસમાં નાખતા ત્રણેય $2000\,^oC$ તાપમાન પ્રાપ્ત કરે તો કયો પદાર્થ વધુ તેજસ્વીતા થી ચળકશે?View Solution
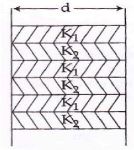
- 6આકૃતિમાં બતાવ્યા પ્રમાણે એક દિવાલમાં એકાંતરે ક્રમશ: $K_1 $ અને $K_2$ ઉષ્મા વાહકતા ધરાવતા $d$ લંબાઇના બ્લોક્સ ધરાવે છે. આ બ્લોક્સના આડછેદના ક્ષેત્રફળ સમાન છે. આ દિવાલની ડાબી અને જમણી બાજુ વચ્ચેની સમતુલ્ય ઉષ્મા વાહકતા કેટલી થાય?View Solution
- 7ગરમ પાણીનું તાપમાન $ {70^o}C $ થી $ {60^o}C $ થતા $5 min$ લાગે છે,તો તાપમાન $ {60^o}C $ થી $ {50^o}C $ થતા લાગતો સમયView Solution
- 8કોલમ $-\,I$ માં અચળાંક અને કોલમ $-\,II$ માં $SI$ એકમો આપેલાં છે, તો યોગ્ય રીતે જોડો :View Solution
કોલમ $-\,I$ કોલમ $-\,II$ $(a)$ વીનનો અચળાંક $(i)$ $Wm^{-2}\,K^{-4}$ $(b)$ સ્ટિફન-બૉલ્ટઝમૅનનો અચળાંક $(ii)$ $Wm^{-1}\,K^{4}$ $(iii)$ $mK$ - 9View Solutionવિધાન : આપેલ તરંગલંબાઇએ જે પદાર્થ ઉષ્માનું ઉત્સર્જન વધુ કરે તે ઉષ્માનો સારો શોષક પણ હોય
કારણ : કિર્ચોફના નિયમ મુજબ આપેલ તરંગલંબાઇએ પદાર્થની ઉત્સર્જકતા અને શોષકતા સમાન હોય
- 10View Solutionશિયાળામાં સવારે ધાતુની સપાટી લાકડાની સપાટી કરતાં વધુ ઠંડી લાગે કારણ કે...