બે દોલિત તંત્ર, એક સાદુ લોલક અને બીજું સ્પ્રિંગ - દળનું લંબવત તંત્ર તેનો પૃથ્વીની સપાટી પર ગતિનો સમયગાળો સરખો છે. તેમને ચંદ્ર પર લઈ જવામાં આવે તો $..................$
Medium
Download our app for free and get started
a
(a)
(a)
For simple pendulum: \(T =2 \pi \sqrt{\frac{\ell}{ g }}\) As g will decrease on moon, time period will increase
For spring mass system : \(T=2 \pi \sqrt{\frac{m}{k}}\)
It will not change and remains the same
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક લોલક ઘડિયાળ $40^o $ $C$ તાપમાને $12$ $s$ પ્રતિદિન ઘીમી પડે છે.તથા $20°$ $C$ તાપમાને $4$ $s$ પ્રતિદિન તેજ થાય છે.આ ઘડિયાળ સાચો સમય બતાવે તે તાપમાન તથા ઘડિયાળના લોલકની ધાતુનો રેખીય-પ્રસરણ ગુણાંક ($\alpha )$ ક્રમશ: છે.View Solution
- 2સરળ આવર્ત ગતિ કરતાં પદાર્થનો મહત્તમ વેગ અને મહત્તમ પ્રવેગ અનુક્રમે $ 2\,m/s $ અને $ 4\,m/{s^2}. $ છે.તો કોણીય વેગ કેટલો ..... $rad/sec$ થાય?View Solution
- 3એક સાદા આવર્ત દોલક માટે વ્યાપક સ્થાનાંતર $x= A \sin \omega t$ છે. ધારો કે $T$ તેનો આવર્તક છે. તેની સ્થિતિઊર્જા $(U)$ - સમય $(t)$ ના વક્રનો ઢાળ, જ્યારે $t=\frac{T}{\beta}$ થાય ત્યારે, મહતમ થાય છે. $\beta$નું મૂલ્ય $..............$ છે.View Solution
- 4એક $m$ દળના કણને પૃથ્વીની ત્રિજ્યા જેટલી ઊંચાઈ $R$ પરથી પૃથ્વીમાં ખોદેલી ટનલમાં આકૃતિમાં દર્શાવ્યા મુજબ છોડવામાં આવે છે. તો સાયું નિવેદન પસંદ કરો.View Solution
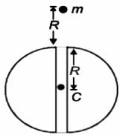
- 5$0.1\, kg$ દળ ધરાવતો કણ $0.1\, m$ ના કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે. જ્યારે આ કણ સમતોલન સ્થાન પાસેથી પસાર થાય ત્યારે તેની ગતિઉર્જા $8\times10^{-3}\; Joule$ જેટલી છે. જો તેની શરૂઆતની કળા $45^o$ હોય તો તેની સરળ આવર્તગતિનું સમીકરણ શું થશે?.View Solution
- 6એક સમક્ષિતિજ પાટીયું $A$ જેટલા કંપવિસ્તારથી ઊપર નીચે સરળ આવર્ત દોલન કરે છે. આ પાટીયાનો સંપર્ક ગુમાવ્યા વગર તેના પર કોઈ પદાર્થ મુકી શકાય તે માટે તેના કંપનનો ન્યુનતમ આવર્તકાળ કેટલો હશે ?View Solution
- 7સમાન આવૃત્તિ અને સમાન કંપવિસ્તાર ધરાવતી બે પરસ્પર લંબ સરળ આવર્ત ગતિ વચ્ચે કળા તફાવત $ \frac{\pi }{2} $ છે, તો પરિણામી ગતિપથ કયા આકારનો થાય?View Solution
- 8$x-$ અક્ષ પર કણનું સ્થાનાંતર $x = a\sin^2 \omega t$ દ્વારા આપવામાં આવે છે. આ કણની ગતિ કોને અનુરૂપ થાય?View Solution
- 9$10$ સેમીનાં કંપવિસ્તાર અને $0.1$ સે. ના આવર્તકાળથી $10$ ગ્રામ દળ ધરાવતો કણ સરળ આવર્તદોલન કરે છે. આ કણ પર લાગતું મહત્તમ બળ (લગભગ) .......... $N$ હશે ?View Solution
- 10પદાર્થ સરળ આવર્ત ગતિ કરે છે. સ્થિતિઉર્જા $(P.E.)$, ગતિઉર્જા $(K.E.)$ અને કુલઉર્જા $(T.E.)$ સ્થાનતર $x$ ના વિધેય સ્વરૂપે માપવામાં આવે છે. નીચેનામાંથી કયું વિધાન સાચું છે?View Solution