બે એકસમાન નળાકાર પાત્રને જમીન પર મૂકેલા છે જેમાં સમાન ઘનતા $d$ ધરાવતું પ્રવાહી ભરેલ છે. બને પાત્રના તળિયાનું ક્ષેત્રફળ $S$ છે પરંતુ એક પાત્રમાં પ્રવાહીની ઊંચાઈ $x_{1}$ અને બીજા પાત્રમાં પ્રવાહીની ઊંચાઈ $x_{2}$ છે. જ્યારે બંને નળાકારને નહિવત કદ ધરાવતી નળી દ્વારા પાત્રના તળીએથી જોડવામાં આવે છે જેથી જ્યાં સુધી બંને પાત્રમાં પ્રવાહી એક નવી ઊંચાઈના સંતુલનમાં ના આવે ત્યાં સુધી પ્રવાહી એક પાત્રમાંથી બીજા પાત્રમાં વહન કરે છે. આ પ્રક્રિયા દરમિયાન તંત્રની ઊર્જામાં કેટલો ફેરફાર થાય?
JEE MAIN 2020, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાણીથી ભરેલ ટાંકીના તળિયે કાણું છે.જો ટાંકીના તળિયે કુલ દબાણ $3\,atm$ હોય ($1\,atm$ $= 10^5\, N/m^2$),તો પ્રવાહનો વેગ કેટલો હશે?View Solution
- 2આકૃતિમાં $2.0\,cm ^2$ આડછેદનું ક્ષેત્રફળવાળા પિસ્ટન દ્વારા નળીમાંથી પ્રવાહી ધકેલાતુ દર્શાવેલ છે. નળીના બાહ્ય છેડાનું આડછેદનું ક્ષેત્રફળ $10\,mm ^2$ છે.જો પિસ્ટનને $4\,cm\,s ^{-1}$ જેટલી ઝડપથી ધકેલવામા આવે, તો બહાર જતા પ્રવાહીની ઝડપ ........ $cm\,s ^{-1}$ છે.View Solution
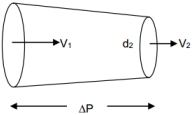
- 3$d_{1}=5$ સેમી $, V_{1}=4$ સેમી $, d_{2}=2$ સેમી ધરાવતી અસમાન આડછેદની નળીના બંન્ને છેડા વચ્ચે દબાણનો તફાવત ........ ($pa$ માં)View Solution
- 4મોટી ટાંકીના આડછેદનું ક્ષેત્ર $0.5 \,m ^{2}$ છે. તેને તળિયા આગળ $1 \,cm ^{2}$ જેટલું આડછેદનું ક્ષેત્રફળ ધરાવતું નાનું છિદ્ર છે. ટાંકીમાં પાણીની ઉપર $25 \,kg$ નો ભાર લગાડવામાં આવે છે. ટાંકીમાં પાણીની ઝડપ અવગણી ટાંકીના તળિયાથી પાણીની ઉંચાઈ $40 \,cm$ હોય ત્યારે છિદ્રમાંથી બહાર આવતાં પાણીનો વેગ ............. $cms ^{-1}$ હશે. $\left[ g =10 \,ms ^{-2}\right.$ લો.]View Solution
- 5એક ઘરની છત પર રહેલી $750\,cm^{2}$ ક્ષેત્રફળ ધરાવતી પાણીની ટાંકીમાં પાણીનું લેવલ પાઈપ ઉપર નળના સ્તરથી ઊંચે રહેલ છે. $500\,nm^2$ આડછેદનું ક્ષેત્રફળ ધરાવતો નળ જ્યારે ખુલ્લો હોય ત્યારે નળમાંથી બાહર નીકળતા પાણીનો વેગ $30\,cm/s$ છે. આ સમયે $\frac{dh}{dt}$ નું મૂલ્ય $x \times 10^{-3}\,m/s$ છે. $x$ નું મૂલ્ય $...........$ હશે.View Solution
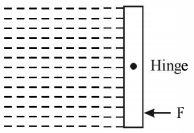
- 6$1\,m \times 1\,m$ $size$ નો ચોરસ ગેટ તેના મધ્યબિંદુથી લટકાવેલ છે.$\rho$ ઘનતાનું પ્રવાહી ગેટની ડાબી બાજુની જગ્યામાં ભરેલ છે. તો ગેટને સ્થિર રાખવા માટે જોઈતું બળ $F . \ldots . .. ....$View Solution
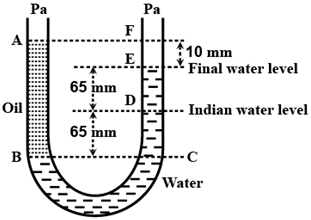
- 7એક $U$ નળી જેના બંને છેડાઓ વાતાવરણ તરફ ખુલ્લા છે, તે આંશિક રીતે પાણીથી ભરેલા છે. પાણી સાથે ન ભળી જાય તેવું તેલ નળીના એક બાજુમાં ત્યાં સુધી ભરવામાં આવે છે, જયાં સુધી બીજી બાજુમાં આવેલા પાણીની સપાટીથી $10\;mm$ ઊંચાઇ પ્રાપ્ત કરી લે છે. આ દરમિયાન પાણી પોતાનો સ્તર $65 \;mm$ જેટલું વધે છે (આકૃતિ જુઓ). તેલની ઘનતા ($kg/m^3$ માં) કેટલી હશે?View Solution
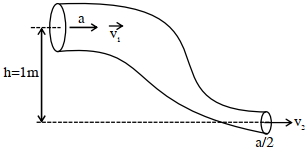
- 8$800 \,kgm ^{-3}$ ઘનતા ઘરાવતું એક આદર્શ પ્રવાહી (આકૃતિમાં દર્શાવ્યા મુજબ) એક વળેલી નળીમાંથી સહેલાઈથી/સરળતાથી વહન પામે છે.આ નળીનો આડછેદ $a$ થી ઘટીને $\frac{a}{2}$ થાય છે. પહોળા અને સાંકળા છેડાઓ વચ્ચે દબાણનો તફાવત $4100 \,Pa$ છે. પહોળા છેડા આગળ પ્રવાહીનો વેગ $\frac{\sqrt{x}}{6} ms ^{-1}$ છે. $x$ નું મૂલ્ય ........ થશે. $\left( g =10 ms ^{-2}\right.$ છે.)View Solution
- 9View Solutionતરલ તેની પોતાની જાતે જ વહનનો વિરોધ કરે તેને શું કહે છે ?
- 10$d,\,2d$ અને $3d$ ઘનતા ધરાવતા ત્રણ પ્રવાહી સમાન દળ લઇને મિશ્રણ કરવાથી, મિશ્રણની ઘનતા કેટલી થાય?View Solution