From the given condition, we have
\(F _{\text {net}}=-\left[2 F _{ q / q } \cos \theta\right]\)
\(F _{\text {net}}=-2 \cdot \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{ q ^{2}}{\left(\sqrt{ d ^{2}+ x ^{2}}\right)^{2}} \cdot \frac{ x }{\sqrt{ d ^{2}+ x ^{2}}}\)
\(=-\frac{q^{2}}{2 \pi \varepsilon_{0}} \frac{x}{\left(d^{2}+x^{2}\right)^{3 / 2}}\)
For \(x ( x << d )\)
\(F_{\text {net }}=-\frac{q^{2}}{2 \pi \varepsilon_{0} d^{3}} x\)
\(\therefore a =-\frac{ q ^{2}}{2 \pi \varepsilon_{0} \cdot md ^{3}} x\)
Comparing with equation of \(SHM \left( a =-\omega^{2} x \right)\)
\(\therefore \omega=\sqrt{\frac{ q ^{2}}{2 \pi \varepsilon_{0} md ^{3}}}\)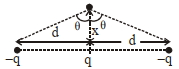
Download our appand get started for free
Similar Questions
- 1$10\, cm$ ત્રિજ્યાનો એક ગોલીય વાહક સમાન રીતે વિતરિત $3.2 \times 10^{-7} \,C$ વિજભાર ધરાવે છે આ ગોળાના કેન્દ્રથી $15 \,cm$ અંતરે રહેલા બિંદુ પર વિદ્યુતક્ષેત્રનું માન શું હશે ?View Solution
$\left(\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} Nm ^{2} / C ^{2}\right)$
- 2$10\,\mu C$ વીજભારને બે ભાગમાં વિભાજીત કરીને $1\,cm$ નાં અંતરે એવી રીતે મૂકવામાં આવે છે, કે જેથી તેના પર લાગતું અપાકર્ષી બળ મહત્તમ હોય. બે ભાગના વીજભાર ......... છે.View Solution
- 3ત્રણ ધન $q$ મૂલ્યના વિજભાર ત્રિકોણના શિરોબિંદુ પર પડેલા છે.તેની પરિણામી બળ રેખા કેવી દેખાય?View Solution
- 4$10\,cm$ ત્રિજયા ધરાવતા સમાન રીતે વિદ્યુતભારીત અવાહક ગોળાથી $20\,cm$ અંતરે વિદ્યુતક્ષેત્ર $100\, V/m$ છે.તો કેન્દ્રથી $3 \,cm$ અંતરે વિદ્યુતક્ષેત્ર કેટલા .....$V/m$ થાય?View Solution
- 5View Solutionવિદ્યુતભારની હાજરીની સાચી કસોટી કઈ છે ?
- 6$L$ મીટર બાજુવાળો ચોરસ પેપરના સમતલમાં છે. સમાન વિદ્યુતક્ષેત્ર $\vec E\;(V/m) $ પેપરના સમતલમાં છે, પણ તે ચોરસના નીચેના અડધા વિસ્તારમાં સીમિત છે. (આકૃતિ જુઓ) પૃષ્ઠ સાથે સંકળાયેલ વિદ્યુતફલક્સ $SI$ એકમમાં કેટલું હશે?View Solution

- 7$6\,m$ ત્રિજ્યા ધરાવતા ગોળાની કદ વિદ્યુતભાર ઘનતા $2\,\mu\,C / cm ^3$ છે. ગોળાની સપાટીમાંથી બહાર આવતી પ્રતિ એકમ પૃષ્ઠ ક્ષેત્રફળ દીઠ બળ રેખાઓની સંખ્યા $..........\times 10^{10} NC ^{-1}$ હશે.View Solution
[Given : Permittivity of vacuum $\left.\epsilon_{0}=8.85 \times 10^{-12} C ^{2} N ^{-1}- m ^{-2}\right]$
- 8View Solutionઆકૃતિ વિદ્યુતક્ષેત્ર સાથે (સંલગ્ન) કેટલીક વિદ્યુત રેખાઓ દર્શાવે છે. તો......
- 9સમાન અને વિરૂદ્ધ વિદ્યુતભારની ઘનતા $\sigma$ વાળી બે અને સમાંતર તકતીઓ એકબીજાથી અંતરે આવેલી છે. તકતીઓના વચ્ચે આવેલ બિંદુ આગળ વિદ્યુતક્ષેત્ર ......... છે.View Solution
- 10વિદ્યુતભાર એ ઈલેક્ટ્રોનીક્સ ભાર $e$ નો પૂર્ણ ગુણાંક છે ઉપરનું વિધાન કોને સાબિત કર્યું છે?View Solution
