બે પ્રક્રિયાઓ $R_1$ અને $R_2$ ના પૂવઘાતાંકીય અવયવો સમાન છે. $R_1$ ની સક્રિયકરણ ઊર્જા $R_2$ કરતા $10\, kJ\,mol^{-1}$ વધારે છે. $300 \,K$ તાપમાને પ્રક્રિયાઓ $R_1$ અને $R_2$ ના વેગ અચળાંક અનુક્રમે $k_1$ અને $k_2$ હોય, તો $\ln (k_2/k_1)$ કોને સમાન થશે ?
JEE MAIN 2017, Diffcult
Download our app for free and get started
d
According to Arrhenius equation
According to Arrhenius equation
\( k=A e^{-E_{2} / R T} \)
\( k_{1} =A e^{-E_{\mathrm{A} 1} / R T} \quad (1)\)
\(k_{2} =A e^{-E_{22} / R T} \quad (2)\)
Dividing Eq. \(( 2 )\) by Eq. \(( 1 )\), we get
\(\frac{k_{2}}{k_{1}}=e^{\left(\frac{E_{21}-E_{22}}{R T}\right)}\)
Taking natural logarithm of both sides, we get
\(\ln \left(\frac{k_{2}}{k_{1}}\right) =\frac{E_{\mathrm{al}}-E_{\mathrm{a} 2}}{R T} \)
\(=\frac{10,000}{8.314 \times 300}=4\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1રાસાયણિક પ્રક્રિયા $2A + 2B + C \rightarrow$ નિપજ માટે સમીકરણને અનુસરતા : $r \propto [A] [B]^2$ પ્રક્રિયાનો ક્રમ......View Solution
- 2જ્યારે તાપમાન વધીને $298\,K$ થી $308 \,K$ થાય ત્યારે તેનો દર બમણો થાય તો પ્રક્રિયાની સક્રિયકરણ ઊર્જા ........... $kJ\, mol^{-1}$ થાય.View Solution
- 3નીચે આપેલી પ્રક્રિયાઓ $NO$ ની $Br_2$ સાથેની પ્રક્રિયા $NOBr$ મેળવવા માટેની છે.View Solution
$NO_{(g)} + Br_{2 (g)} $ $\rightleftharpoons$ $ NOBr_{2 (g)} , NOBr_{2 (g)} + NO_{(g)}\rightarrow 2 NOBr_{(g)}$ જો બીજી પ્રક્રિયાએ વેગનિર્ણાયક તબક્કો હોય તો પ્રક્રિયાનો ક્રમ $NO_{(g)} $ ના સંદર્ભમાં........ હશે.
- 4$975\, {~K}$ પર નીચે આપેલ રાસાયણિક પ્રક્રિયા માટે નીચેની માહિતી મેળવવામાં આવ્યો હતો.View Solution
$2 {NO}_{({g})}+2 {H}_{2({~g})} \rightarrow {N}_{2({~g})}+2 {H}_{2} {O}_{({g})}$
$[NO]$
${mol} {L}^{-1}$
${H}_{2}$
${mol} {L}^{-1}$
વેગ
${mol}L^{-1}$ $s^{-1}$
$(A)$ $8 \times 10^{-5}$ $8 \times 10^{-5}$ $7 \times 10^{-9}$ $(B)$ $24 \times 10^{-5}$ $8 \times 10^{-5}$ $2.1 \times 10^{-8}$ $(C)$ $24 \times 10^{-5}$ $32 \times 10^{-5}$ $8.4 \times 10^{-8}$ ${NO}$ના સંદર્ભમાં પ્રક્રિયાનો ક્રમ $....$ છે.
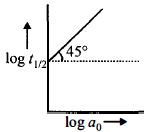
- 5પ્રક્રિયા $A \to$ નીપજો માટે $log\,t_{1/2}$, વિરુદ્ધ $log\,a_0$ નો આલેખ આકૃતિમાં દર્શાવ્યો છે. જો $A$ ની શરૂઆતની સાંદ્રતા $a_0,$, વડે દર્શાવવામાં આવે તો પ્રક્રિયાની ક્રમ જણાવો.View Solution
- 6આપેલ આલેખ બે જુદી જુદી પ્રક્રિયા $(i)$ અને $(ii)$ માટે સમય સાથે પ્રક્રિયક $R$ ની સાંદ્રતાનો ફેરફાર રજૂ કરે છે. તી પ્રક્રિયાના ક્રમ અનુક્રમે જણાવો.View Solution
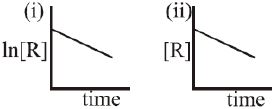
- 7${25\,^o}C$ તાપમાને એક પ્રક્રિયાનો વેગ અચળાંક, સક્રિયકરણ ઊર્જા, અને આર્હેનિયસ માપદંડ અનુક્રમે $3.0 \times {10^{ - 4}}\,{s^{ - 1}}$, $104.4\,kJ\,mo{l^{ - 1}}$ અને $6.0 \times {10^{14}}\,{s^{ - 1}}$ છે. તો $T \to \infty $ પર વેગઅચળાંકની કિંમત શું થશે ?View Solution
- 8પ્રથમ ક્રમ પ્રક્રિયા માટે, $75 \,\%$ પૂર્ણ થવા માટેનો સમય અને $50\, \%$ પૂર્ણ થવા માટેનો સમયનો ગુણોત્તર $....$ છે. (પૂર્ણાંકમાં જવાબ)View Solution
- 9$50\,mm$ $AB_3$ નું ઉદ્દીપકીય વિઘટન માટે અદ્ય આયુ સમય $4$ કલાક અને $100\,mm$ એ તેને $2$ કલાક લાગે છે તો પ્રક્રિયાનો ક્રમ..... થશે?View Solution
- 10$25^{\circ} C$ પર $3.33\, h$ અર્ધ-આયુષ્ય સાથે, સુક્રોઝ એસિડ દ્રાવણમાં ગ્લૂકોઝ અને ફ્રૂકટોઝમાં જળવિભાજન પામે છે જે પ્રથમ ક્રમ વેગ નિયમને અનુસરે છે. $9\, h$ પછી, સુક્રોઝનો અંશ $f$ બાકી રહે છે. તો $\log _{10}\left(\frac{1}{f}\right)$ નું મૂલ્ય ..... $\times 10^{-2}$ છે.View Solution
(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ) (ધારી લો : $\ln 10=2.303, \ln 2=0.693$)