Let \(P_i\) and \(R_i\) be the inside pressure and radius of the ith soap bubble respectively.
\(\therefore {P_1} = P + \frac{{4T}}{{{R_1}}}.\,\,\,{P_2} = P + \frac{{4T}}{{{R_2}}}\,\,and\,\,{P_3} = P + \frac{{4T}}{{{R_3}}}\)
\(Also\,{P_1}{V_1} + {P_2}{V_2} = {P_3}{V_3}\)
\(\therefore \left( {P + \frac{{4T}}{{{R_1}}}} \right)\frac{{4\pi }}{3}R_1^3 + \left( {P + \frac{{4T}}{{{R_2}}}} \right)\frac{{4\pi }}{3}R_2^3\)
\( = \left( {p + \frac{{4T}}{{{R_3}}}} \right)\frac{{4\pi }}{3}R_3^3\)
\(P\left( {\frac{{4\pi }}{3}R_1^3 + \frac{{4\pi }}{3}R_2^3 - \frac{{4\pi }}{3}R_3^2} \right)\)
\( + \frac{{4T}}{3}\left( {4\pi R_1^2 + 4\pi R_2^2 - 4\pi R_3^2} \right) = 0\)
\(P\left( {{V_1} + {V_2} - {V_3}} \right) + \frac{{4T}}{3}\left( {{S_1} - {S_2} - {S_3}} \right) = 0\)
\(PV + \frac{{4T}}{3}S = 0\,\,\,\,\,\,\, \Rightarrow \,\,\,\,3PV + 4ST = 0\)
Download our appand get started for free
Similar Questions
- 1પાણીમાં $20\,cm$ લંબાઇની કેશનળી ડુબાડતાં $8\,cm$ ઊંચાઇ સુધી પાણી ઉપર આવે છે. જો મુકત પતન કરતી લિફ્ટમાં પાણીમાં કેશનળી ડુબાડતાં ...... $cm$ ઊંચાઇ સુધી પાણી આવશે?View Solution
- 2View Solutionરેઈનકોટ્સને ક્યા દ્રવ્યો (પદાર્થો) સાથે કોટિંગ દ્વારા વોટરપ્રૂફ બનાવવામાં આવે છે ?
- 3$30 \,dynes\, per\, cm $ પૃષ્ઠતાણ ધરાવતા $\frac{1}{{\sqrt \pi }}\,cm$ ત્રિજયાના પરપોટાની ત્રિજયા $\frac{2}{{\sqrt \pi }}\,cm$ કરવા માટે ....... $ergs$ કાર્ય કરવું પડે.View Solution
- 4નીચે બે વિધાનો આપેલા છે :View Solution
વિધાન $I$: જ્યારે કેશનળીને પ્રવાહીમાં ડૂબાડવામાં આવે છે ત્યારે પ્રવાહી કેશનળીમાં ઉપર ચઢતું નથી કે નીચે પણ ઉતરતું નથી. સંપર્કકોણ $0^{\circ}$ હોય શકે છે.
વિધાન $II$ : ધન અને પ્રવાહી વચ્ચેનો સંપર્કકોણ ધન દ્રવ્યના અને પ્રવાહી દ્રવ્યના ગુણધર્મ પર પણ આધારીત છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભરમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 5View Solutionએક યાંત્રિક પંપ વડે નળીના છેડા (મુખ) આગળ બનાવેલ સાબુના પરપોટાનું કદ એ અચળ દરે વધે છે. પરપોટાની અંદરના દબાણનું સમય પરનો આધાર સાચી રીતે દર્શાવતો આલેખ_________ મુજબ આપી શકાય
- 6કેશનળીને શિરોલંબ સાથે ${30^o}$ અને ${60^o}$નો ખૂણો બનાવે તે રીતે ગોઠવેલ છે. તો કેશનળીમાં પ્રવાહીની લંબાઇનો ગુણોતર કેટલો થાય?View Solution
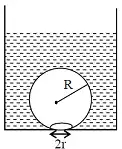
- 7પાણીને ગરમ કરતાં પાત્રને તળિયે બનેલું પરપોટું પાત્રથી અલગ થઈને ઉપર આવે છે. પરપોટાની ત્રિજ્યા $R$ અને પાત્રના તળિયા સાથેના વર્તુળાકાર સંપર્કની ત્રિજ્યા $r$ લો. જો $r < < R$ અને પાણીનું પૃષ્ઠતાણ $T$ હોય, તો પરપોટું પાત્રથી અલગ પડે તેની માત્ર પડેલા $r$ નું મૂલ્ય કેટલું હશે?(પાણીની ઘનતા $\rho_{w}$ છે)View Solution
- 8$5 \,N/m$ પૃષ્ઠતાણ ધરાવતા પ્રવાહીમાંથી $0.02 \,m^2 $ ક્ષેત્રફળ ધરાવતી ફિલ્મ બનાવવા માટે કેટલી ઉર્જાની જરૂર પડે?View Solution
- 9નીચે બે વિધાનો આપેલા છે : એકને કથન $A$ અને બીજાને કારણ $R$ વડે દર્શાવવામાં આવ્યા છે.View Solution
કથન $(A)$ : કપડાં પર પડેલા તેલના કે ગ્રીસના ડાધા પાણીથી ધોવાથી દૂર થતા નથી.
કારણ $(R)$ : કારણ કે તેલ અથવા ગ્રીસ અને પાણી વચ્ચેનો સંપર્કકોણ બહુકોણ $(obtuse)$ હોય છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી સાચો વિકલ્પ પસંદ કરો :
- 10જો સાબુના પરપોટાની અંદર વધારાના દબાણને $2\; mm$ ઊંંચાઈના તેલના સ્તંભ વડે સંતુલિત કરવામાં આવે છે તો પછી સાબુના દ્રાવણનું પૃષ્ઠતાણ કેટલું હશે? ($r=1\; cm$, તેલની ઘનતા = $\left.0.8 \;g / cm ^3\right)$View Solution
