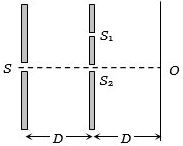
બે સ્લિટ $S_1$ અને $S_2$ વચ્ચેનું અંતર $d $ છે,તો $d $ ની કઇ લઘુત્તમ કિંમત માટે $O $ બિંદુ અપ્રકાશિત થાય?

Diffcult
c
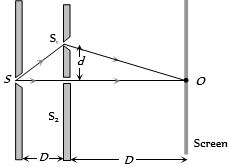
(c)Path difference between the waves reaching at\(P,\)\(\Delta = {\Delta _1} + {\Delta _2}\)
where\({\Delta _1} = \) Initial path difference
\({\Delta _2} = \)Path difference between the waves after emerging from slits.
\({\Delta _1} = S\,{S_1} - S\,{S_2} = \sqrt {{D^2} + {d^2}} - D\)
and \({\Delta _2} = {S_1}O - {S_2}O = \sqrt {{D^2} + {d^2}} - D\)
\(\therefore \,\,\,\Delta = 2\left\{ {{{({D^2} + {d^2})}^{\frac{1}{2}}} - D} \right\} = 2\left\{ {({D^2} + \frac{{{d^2}}}{{2D}}) - D} \right\}\)
\( = \frac{{{d^2}}}{D}\) (From Binomial expansion)
For obtaining dark at \(O\), \(\Delta \) must be equals to \((2n - 1)\frac{\lambda }{2}\) i.e. \(\frac{{{d^2}}}{D} = (2n - 1)\frac{\lambda }{2} \Rightarrow d\sqrt {\frac{{(2n - 1)\lambda \,D}}{2}} \)
For minimum distance \(n = 1\) so \(d = \sqrt {\frac{{\lambda \,D}}{2}} \)
(c)Path difference between the waves reaching at\(P,\)\(\Delta = {\Delta _1} + {\Delta _2}\)
where\({\Delta _1} = \) Initial path difference
\({\Delta _2} = \)Path difference between the waves after emerging from slits.
\({\Delta _1} = S\,{S_1} - S\,{S_2} = \sqrt {{D^2} + {d^2}} - D\)
and \({\Delta _2} = {S_1}O - {S_2}O = \sqrt {{D^2} + {d^2}} - D\)
\(\therefore \,\,\,\Delta = 2\left\{ {{{({D^2} + {d^2})}^{\frac{1}{2}}} - D} \right\} = 2\left\{ {({D^2} + \frac{{{d^2}}}{{2D}}) - D} \right\}\)
\( = \frac{{{d^2}}}{D}\) (From Binomial expansion)
For obtaining dark at \(O\), \(\Delta \) must be equals to \((2n - 1)\frac{\lambda }{2}\) i.e. \(\frac{{{d^2}}}{D} = (2n - 1)\frac{\lambda }{2} \Rightarrow d\sqrt {\frac{{(2n - 1)\lambda \,D}}{2}} \)
For minimum distance \(n = 1\) so \(d = \sqrt {\frac{{\lambda \,D}}{2}} \)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\lambda$ તરંગલંબાઈ સાથે યંગના ડબલ સ્લિટ પ્રયોગમાં તો પડદા પર રચાતી શલાકાની ભાતમાં શલાકાની પહોળાઈ $\beta $ છે. જ્યારે બે $t_1$ અને $t_2 (t_1 > t_2)$ જાડાઈની કાચની બે પ્લેટો (વક્રીભવનાંક $\mu$ ) ને અનુક્રમે બે પ્રકાશ પુંજના માર્ગમાં મૂકવામાં આવે તો શલાકાની ભાત કેટલા અંતરે ખસેલી હશે?View Solution
- 2યંગના દ્વિ સ્લીટ પ્રયોગમાં, આ સ્લીટો $2 \,mm$ ની છે અને તે બે તરંગલંબાઈ $\lambda= 7500 \,Å$ અને $\lambda = 9000\, Å$ ના મિશ્રણથી પ્રકાશિત કરેલ છે. સ્લીટથી $2 \,m$ દૂર પડદા ના સામાન્ય કેન્દ્રથી કેટલા......$mm$ અંતરે એક વ્યતિકરણ ભાતમાંની પ્રકાશિત શલાકા બીજામાંની પ્રકાશિત શલાકા સાથે સુસંગત થશે?View Solution
- 3શૂન્યઅવકાશમાં સમાન તરંગલંબાઈ $\lambda$ ધરાવતા બે તરંગો છે. એક તરંગ $n_{1}$ વક્રીભવનાંક ધરાવતા માધ્યમ માં $L _{1}$ અંતર અને બીજું તરંગ $n_{2}$ વક્રીભવનાંક ધરાવતા માધ્યમમાં $L _{2}$ અંતર કાપ્યા પછી બંને તરંગો વચ્ચે કળા તફાવતView Solution
- 4યંગના ડબલ સ્લિટના પ્રયોગમાં $4000 \,Å$ તરંગલંબાઇ માટે શલાકાની પહોળાઇ $0.6\, mm$ છે.હવે,પ્રયોગ પાણીમાં કરતાં શલાકાની પહોળાઇ....$mm$View Solution
- 5યંગના પ્રયોગમાં $5$મી અપ્રકાશીત શલાકા મધ્યસ્થ પ્રકાશીત શલાકાથી $4 \,mm$ છે,જો $D =2\, m , \lambda=$ $600\, nm ,$ હોય તો બે સ્લીટ વચ્ચેનું અંતર($mm$ માં) કેટલું હશે?View Solution
- 6View Solutionપોલારાઇઝર પર ધ્રુવીભૂત પ્રકાશ આપાત કરવામાં આવે છે.આપાતકિરણને અક્ષ તરીકે લઇને પોલારાઇઝરના એક પરિભ્રમણ દરમિયાન...
- 7$4I$ અને $9I$ તીવ્રતા ધરાવતા બે પ્રકાશ, પડદા ઉપર વ્યતિકરણ અનુભવે છે. પડદા ઉપર $A$ બિંદુ આગળ કળા તફાવત શૂન્ય. અને બિંદુ $B$ આગળ $\pi$ છે. બિંદુ $A$ અને $B$ આગળ પરિણામી તીવ્રતાઓનો તફાવત $........\,I$ થશે.View Solution
- 8માઇક્રોસ્કોપમાં રહેલ વસ્તુકાંચનો વ્યાસ મુખ્યકેન્દ્ર સાથે $\beta $ ખૂણો બનાવે છે. વસ્તુ અને લેન્સ વચ્ચેનું માધ્યમ તેલ છે જેનો વક્રીભવનાંક $n$ છે. તો માઇક્રોસ્કોપનો વિભેદન પાવર ....View Solution
- 9View Solutionહાઈગેનનો સિદ્ધાંત ...........ને લાગુ પાડી શકાય.
- 10View Solutionફેશનલ બાયપ્રિઝમ ના પ્રયોગમાં નીચેનામાંથી ક્યો પ્રકાશ ઉદ્દગમ કેન્દ્રીય શલાકાને દર્શાવવા વાપરવામાં આવે છે?
