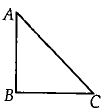
બે સમાન વર્તુળાકાર ગુંચળા $P$ અને $Q$ મા આંટાની સંખ્યા $100$ અને ત્રિજયા $\pi \mathrm{cm}$ છે. $P$ અને $Q$ માં વિદ્યુત પ્રવાહ અનુક્રમે $1 \mathrm{~A}$ અને $2 \mathrm{~A}$ છે. ગુંચળા $\mathrm{P}$ અને $Q$ તેમના કેન્ટ્રો સંપાત થાય તથા તેમના સમતલો પરસ્પર લંબ રહે તે રીતે ગોઠવેલ છે. જો આ ગૂંચળાના સામાન્ય
કેન્દ્ર પર ચુંબકીય ક્ષેત્ર $\sqrt{\mathrm{X}} \mathrm{mT}$ હોય તો $\mathrm{X}=$.....
$\left[\mu_0=4 \pi \times 10^{-7} \mathrm{TmA}^{-1}\right]$
JEE MAIN 2024, Diffcult
b
\(\mathrm{B}_{\mathrm{p}}=\frac{\mu_0 \mathrm{Ni}_1}{2 \mathrm{r}}=\frac{\mu_0 \times 1 \times 100}{2 \pi}=2 \times 10^{-3} \mathrm{~T}\)
\(\mathrm{B}_{\mathrm{p}}=\frac{\mu_0 \mathrm{Ni}_1}{2 \mathrm{r}}=\frac{\mu_0 \times 1 \times 100}{2 \pi}=2 \times 10^{-3} \mathrm{~T}\)
\(\mathrm{~B}_{\mathrm{Q}}=\frac{\mu_0 \mathrm{Ni}_2}{2 \mathrm{r}}=\frac{\mu_0 \times 2 \times 100}{2 \pi}=4 \times 10^{-3} \mathrm{~T}\)
\(\mathrm{~B}_{\text {net }}=\sqrt{\mathrm{B}_{\mathrm{p}}^2+\mathrm{B}_{\mathrm{Q}}^2}\)
\(=\sqrt{20} \mathrm{mT}\)
\(\mathrm{x}=20\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન ચુંબકીય ક્ષેત્ર ૠણ $X$ દિશામાં પ્રવર્તમાન છે.એક વિદ્યુતભાર આ ચુંબકીય ક્ષેત્રમાં $X$ દિશામાં ગતિ કરતો કરતો દાખલ થાય છે,પરિણામે ...View Solution
$X$-દિશામાં $v$ વેગ સાથે ગતિ કરતો વિદ્યુતભાર ઋણ $X$ દિશામાં રહેલા ચુંબકીયક્ષેત્રને આધિન ગતિ કરે છે. પરિણામે, વિદ્યુતભાર ...
- 2$d$ અંતરે રહેલા બે લાંબા સમાંતર તારમાંથી પસાર થતા પ્રવાહ $I_1$ અને $I_2$ છે.બંને પ્રવાહ એક જ દિશામાં હોય,તો તાર વચ્ચે લાગતું બળ $F$ છે.હવે એક પ્રવાહનું મૂલ્ય બમણું અને દિશા વિરુધ્ધ કરવામાં આવે છે.બંને તારને $3\,d$ અંતરે મૂકતાં નવું બળ કેટલું થશે?View Solution
- 3જ્યારે વિદ્યુતભારિત કણ $\overrightarrow{v}$ વેગથી $\overrightarrow{B}$ જેટલા ચુંબકીયક્ષેત્રમાં ગતિ કરે ત્યારે તેના પર લાગતું બળ શૂન્ય નથી, તો તે બતાવે છે કેView Solution
- 4View Solutionવિદ્યુતપ્રવાહ ધારિત તારમાં કુલ વિદ્યુતભાર શૂન્ય છે તેમ છતાં ચુંબકીય ક્ષેત્ર તેના પર બળ લગાટે છે, કારણ કે ચુંબકીય ક્ષેત્ર
- 5$a$ ત્રિજ્યા ધરાવતું વર્તુળાકાર લૂપમાંથી $I$ પ્રવાહ પસાર થાય છે.તેને $\mathrm{B}$ જેટલા ચુંબકીય ક્ષેત્રમાં લૂપના સમતલને લંબ એવીરીતે મૂકવામાં આવે છે જેથી તેના વ્યાસને અનુલક્ષીને નાનો ખૂણો બનાવીને મુક્ત કરવામાં આવે તો તે $T$ આવર્તકાળ સાથે સરળ આવર્તગતિ કરે છે.જો લૂપની દળ $m$ હોય તો તેનો આવર્તકાળ કેટલો થાય?View Solution
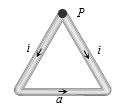
- 6$'a' $ બાજુવાળા સમબાજુ ત્રિકોણમાં $i $ પ્રવાહનું વહન થાય છે.ત્રિકોણના બિંદુ $P$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 7View Solutionએક વિદ્યુતભારિત કણ ચુંબકીય ક્ષેત્રને લંબ ગતિ કરે છે, તો .....
- 8એક લાંબા સોલેનોઈડમાં $200$ આંટાઓ પ્રતિ $cm$ છે તથા પ્રવાહ $i$ છે. તેનાં મધ્યબિંદુ આગળ ચુંબકીયક્ષેત્ર $6.28 \times 10^{-2}\; Weber / m ^{2}$ છે. બીજા એક લાંબો સોલેનોઈડ $100$ આંટાઓ પ્રતિ $cm$ અને $\frac i3$ જેટલો પ્રવાહ ધરાવે છે. તો તેના મધ્યબિંદુ આગળ ચુંબકીયક્ષેત્ર કેટલું હશે?View Solution
- 9વીજપ્રવાહ ધારિત લંબ ચોરસ લૂપ $PQRS$ સમાન તારની બનેલી છે. $P R=Q S=5\,cm$ અને $P Q=R S=100\,cm$ છે. જો એમિટર પ્રવાહનું અવલોકન $I$ થી $2I$ બદલાય તો તાર $PQ$ પર તાર $RS$ ને લીધે લાગુ પડતા પ્રતિ લંબાઈ ચુંબકીયબળનો ગુણોત્તર $\left(f_{P Q}^I: f_{P Q}^{2 I}\right)$ $................$ થાય.View Solution
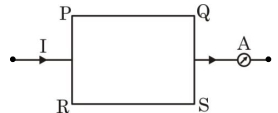
- 10કાટકોણ સમદ્વિબાજુ ત્રિકોણ $ABC$ ને સમાન ચુંબકીયક્ષેત્રની દિશા $AB$ ને સમાંતર રહે તેમ મૂકેલ છે. જો $ BC$ બાજુ પર ચુંબકીય બળ $\vec F$ લાગતું હોય, તો $AC$ બાજુ પર લાગતું બળ કેટલું થાય?View Solution