બે સુસમ્બદ્વ ઉદ્ગમોની તીવ્રતાનો ગુણોત્તર $\alpha $ છે.$\frac{{{I_{max}} - {I_{min}}}}{{{I_{max}} + {I_{min}}}}$ નું મૂલ્ય કેટલું થાય?
NEET 2017,NEET 2016,AIIMS 2016, Medium
a
\(\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }}=\frac{\left(a_{1}+a_{2}\right)^{2}-\left(A_{1}-A_{2}\right)^{2}}{\left(A_{1}+A_{2}\right)^{2}+\left(A_{1}-A_{2}\right)^{2}}\)
\(\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }}=\frac{\left(a_{1}+a_{2}\right)^{2}-\left(A_{1}-A_{2}\right)^{2}}{\left(A_{1}+A_{2}\right)^{2}+\left(A_{1}-A_{2}\right)^{2}}\)
\(I_{\max }=\left(A_{1}+A_{2}\right)^{2}, I_{\min }=\left(A_{1}-A_{2}\right)^{2}\) where
\(A=\)amplitude
\(=\frac{4 A_{1} A_{2}}{2\left(A_{1}^{2}+A_{2}^{2}\right)}=\frac{2 A_{1} A_{2}}{A_{1}^{2}+A_{2}^{2}}\)
Now, dividing the numerator and denominator by \(A _{1} A _{2}\), we get
\(\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }}=\frac{2}{\left[\frac{A_{1}}{A_{2}}+\frac{A_{2}}{A_{1}}\right]}=\frac{2}{\left[\sqrt{\alpha}+\frac{1}{\sqrt{\alpha}}\right]}=\frac{2 \sqrt{\alpha}}{(\alpha+1)}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
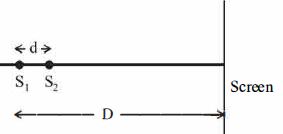
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે બે સુસમ્બદ્ધ ઉદ્ગમો $S_1$ અને $S_2$ ખૂબ નાના અંતર $ ‘d’$ થી અલગ કરેલા છે.પડદા પર ઉત્પન્ન શલાકાઓ _____ હશે.View Solution
- 2સ્લિટની પહોળાઇ $ 12 \times {10^{ - 5}}cm. $ અને પ્રકાશની તરંગલંબાઇ $ 6000\,{Å} $ છે,તો મધ્યસ્થ અધિકતમની પહોળાઇ કેટલા ......$ rad$ થાય?View Solution
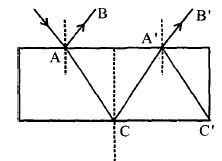
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $I$ તીવ્રતા ધરાવતું પ્રકાશનું કિરણ $A$ બિંદુ આગળ આપાત થાય છે. જેનું પાશ્વિક પરાવર્તન અને પાશ્વિક વક્રીભવન થાય છે. દરેક પરાવર્તન સમયે $25\%$ આપાત પ્રકાશની તીવ્રતાનું પરાવર્તન થાય છે. કિરણ $AB$ અને $A'B'$ વ્યતિકરણ અનુભવે, તો $I_{max}$ અને $I_{min}$ નો ગુણોત્તર કેટલો મળે?View Solution
- 4યંગના બે સ્લિટનાં પ્રયોગમાં $5000 A ̊$ તરંગલંબાઈ ધરાવતા એકરંગી પ્રકશનો ઉપયોગ કરવામાં આવે છે. સ્લિટ એબીજાની 1.0 $\mathrm{mm}$ અંતરે અને પડદો સ્લિટ થી $1.0 \mathrm{~m}$ અંતરે છે. પડદાના કેન્દ્રે કે જ્યાં પ્રથમ વખત મહતમ તીવ્રતા કરતાં અડધી થાય નું અંતર_________$\times 10^{-6} \mathrm{~m}$છે.View Solution
- 5View Solutionઉનાળાની ગરમ રાત્રે હવાનો વક્રીભવનાંક જમીનની નજીક લઘુતમ હશે અને જમીનથી ઉપર ઊંચાઇ સાથે વધતો જોય છે.હાઇગેનના સિદ્વાંત પરથી આપણે તારણ કાઢી શકીએ કે જયારે પ્રકાશ કિરણને સમક્ષિતિજ દિશામાં આપાત કરતાં,તે જયારે પ્રસરતું હોય ત્યારે કિરણપુંજ ________
- 6બે પોલેરોઈડની અક્ષ એકબીજાને સમાંતર છે જેથી તેમાંથી નીકળતા પ્રકાશની તીવ્રતા મહત્તમ મળે. તો કોઈ પણ એક પોલેરોઈડને કેટલા $^o$ ના ખૂણે ફેરવવો જોઈએ કે જેથી તેમાંથી નીકળાતા પ્રકાશની તીવ્રતા અડધી થાય?View Solution
- 7યંગના પ્રયોગમાં, જયાં પથતફાવત $\lambda$ . હોય ત્યાં તીવ્રતા $k$ છે.જયાં પથતફાવત $\lambda /4$ હોય ત્યાં તીવ્રતા કેટલી હશે? ( $λ=$ પ્રકાશની તરંગલંબાઇ)View Solution
- 8.......$^o$ ખૂણે પ્રકાશ આપાત કરતા પાણીમાંથી પરાવર્તન પામતો પ્રકાશ સંપૂર્ણ તલધ્રુવીભૂત હશે?View Solution
- 9વિધાન $-I:$ કેલ્સાઈટ સ્ફટિક વડે સ્વચ્છ આકાશનું અવલોકન કરતાં જાણવા મળે છે કે, સ્ફટિકને ગોળ ગોળ ઘૂમાવતાં પસાર થતા પ્રકાશની તીવ્રતા બદલાય છે.View Solution
વિધાન $-II:$ વાતાવરણના કણો દ્વારા સૂર્યપ્રકાશનું પ્રકીર્ણન થવાથી આકાશમાંથી આવતો પ્રકાશ ધ્રુવીભૂત થયેલો હોય છે. વાદળી રંગના પ્રકાશનું પ્રકીર્ણન સૌથી વધારે થાય છે.
- 10View Solutionએક સ્લિટ વિવર્તનના પ્રયોગમાં બીજી મહતમ મેળવવાની શરત
