બે પોલેરોઈડની અક્ષ એકબીજાને સમાંતર છે જેથી તેમાંથી નીકળતા પ્રકાશની તીવ્રતા મહત્તમ મળે. તો કોઈ પણ એક પોલેરોઈડને કેટલા $^o$ ના ખૂણે ફેરવવો જોઈએ કે જેથી તેમાંથી નીકળાતા પ્રકાશની તીવ્રતા અડધી થાય?
AIEEE 2012, Medium
Download our app for free and get started
a
For \(I = \frac{{{I_0}}}{2}\) and \(I = {I_0}\,{\cos ^2}\,\theta = \frac{{{I_0}}}{2}\) \(\therefore \theta = {45^o}\) Therefore the angle through which either polaroids turned is \(135^o (= 180^o -45^o)\)
For \(I = \frac{{{I_0}}}{2}\) and \(I = {I_0}\,{\cos ^2}\,\theta = \frac{{{I_0}}}{2}\) \(\therefore \theta = {45^o}\) Therefore the angle through which either polaroids turned is \(135^o (= 180^o -45^o)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1યંગનો પ્રયોગ $4360 \;\mathring A$ અને $5460 \;\mathring A$ ની તરંગલંબાઈના વાદળી અને લીલા પ્રકાશ સાથે કરવામાં આવે છે. જો મઘ્યબિંદુથી ચૌથી પ્રકાશિત શલાકાનું સ્થાન $x$ હોય, તોView Solution
- 2View Solutionવિવર્તન ભાતમાં કેન્દ્રીય મહત્તમની કોણીય પહોળાઈ એક સ્લીટ માટે .........પર આધાર રાખતી નથી.
- 3સ્લિટ દ્વારા થતા ફ્રોનહોફર વિવર્તનમાં, જો સ્લીટની પહોળાઈ $a$, તરંગલંબાઈ $\lambda$, અને લેન્સની કેન્દ્રલંબાઈ $f$ હોય તો કેન્દ્રીય મહત્તમની રેખીય પહોળાઈ.....View Solution
- 4એક સિંગલ (એક) સ્લિટનાં પ્રયોગમાં, $550 \mathrm{~nm}$ તરંગલંબાઈ ધરાવતી લીલા રંગની કિરણાવલી $0.20 \mathrm{~mm}$ પહોળાઈ ધરાવતી સ્લિટ માંથી પસાર થાય છે. નિર્ગમન પામતો પ્રકાશ $100 \mathrm{~cm}$ દૂર રાખેલા પડદા ઉપર એકઠો કરવામાં આવે છે. મધ્યસ્થ અધિક્તમ થી પ્રથમ ક્રમનું ન્યૂનતમ $x$. . . . . . .$\times 10^{-5} \mathrm{~m}$ અંતરે મળે છે, $x$ નું મૂલ્ય. . . . . .હશે.View Solution
- 5યંગના પ્રયોગમાં એક પાતળી અબરખની $12 \times 10^{-7} m$ જાડાઈની શીટ વ્યતિકારી કિરણોમાંના કોઈ એક કિરણના પથમાં મૂકવામાં આવે છે. એવું જાણવા મળે છે કે કેન્દ્રિય પ્રકાશિત પટ્ટો પ્રકાશિત શલાકાની પહોળાઈ જેટલું અંતર ખસે છે. જો $6 \times 10^{-7}m $તરંગલંબાઈવાળો પ્રકાશ હોય તો અબરખનો વક્રીભવનાંક શોધો.View Solution
- 6View Solutionયંગના પ્રયોગમાં એકસરખી જાડાઈની બે સ્લિટ લેવાના બદલે એક સ્લિટ, બીજી સ્લિટ કરતાં બમણી પહોળાઈની છે, તો વ્યતિકરણ શલાકાઓમાં ...
- 7View Solutionસાબુની પાતળી પટ્ટી પર અપ્રકાશિત અને રંગીન ભાત શાના કારણો જેવા મળે છે?
- 8View Solutionતરંગ અગ્રનો અર્થ શું થાય?
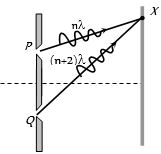
- 9યંગના ડબલ સ્લિટના પ્રયોગમાં $PX $ અને $QX$ પથની લંબાઇ $ n\lambda $ અને $ (n + 2)\lambda $ છે,મધ્ય શલાકાની તીવ્રતા શૂન્ય હોય,તો $X $ આગળ...View Solution
- 10View Solutionગૌણ તરંગોનો હાઈગેંસનો વિચાર