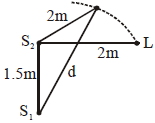
બે સુસંબંધ ધ્વનિ ઉદગમાં $s_1$ અને $S_2$ એ $1\,m$ તરંગલંબાઈ ધરાવતા સમાન કળાના તરંગો ઉત્પન્ન કરે છે $S_{1}$ અને $S_{2}$ ને $1.5\,cm$ અંતરે રાખેલા છે. $S_{2}$ ની સામે $2\,m$ અંતરે રહેલા અવલોકનકાર $L$ ને લઘુતમ તીવ્ર્તાનો અવાજ સંભળાઈ છે જ્યારે અવલોકનકાર $S_1$ થી દૂર તરફ પરંતુ $S_2$ થી સમાન અંતરે રહીને ગતિ કરે ત્યારે તે જ્યારે $S_1$ થી $d$ અંતરે હોય ત્યારે મહતમ તીવ્ર્તા સંભળાઈ છે તો $d=......m$

JEE MAIN 2020, Diffcult
b
Initially \(S _{2} L =2 m\)
Initially \(S _{2} L =2 m\)
\(S_{1} L=\sqrt{2^{2}+(3 / 2)^{2}}\)
\(S_{1} L=\frac{5}{2}=2.5 m\)
\(\Delta x =S_{1} L -S_{2} L =0.5 m\)
So since \(\lambda=1 m \quad \therefore \Delta x =\frac{\lambda}{2}\)
So while listener moves away from \(S_{1}\)
Then, \(\Delta x\left(=S_{1} L-S_{2} L\right)\) increases
and hence, at \(\Delta x=\lambda\) first maxima will appear. \(\Delta x=\lambda=S_{1} L-S_{2} L\)
\(1=d-2 \Rightarrow d=3 m\)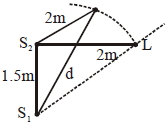
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1યંગના બે સ્લિટના પ્રયોગમાં, જ્યાં પથ તફાવત $\lambda$ છે. ત્યાં તીવ્રતા $K$ છે. તો જ્યારે પથ તફાવત $\lambda /4 $ હોય, તો ત્યારે તીવ્રતા .....View Solution
- 2યંગના ડબલ સ્લીટના પ્રયોગમાં બે અલગ અલગ તરંગલંબાઈ $500\,nm$ અને $600\, nm$ નો ઉપયોગ કરવામાં આવે છે જે પોતાની ભાત પડદા પર પાડે છે. આ ભાતની મધ્યમાં જ્યાં પથ તફાવત શૂન્ય છે ત્યાં બંનેની ભાતના મહત્તમ સંપાત થાય છે જે વ્યતિકરણ અનુભવે છે જેનાથી મળતું પરિણામી બીજા કરતાં સ્પષ્ટ દેખાય છે. પરંતુ જ્યારે એક આ મધ્યમાન ક્ષેત્રમાંથી બહાર આવે ત્યારે બે શલાકાના તંત્રમાં એક તરંગલંબાઈનું મહત્તમ બીજી તરંગલંબાઈના ન્યૂનતમ સાથે સંપાત થાય છે. અને મળતું શલાકાનું તંત્ર અસ્પષ્ટ દેખાય છે. આવું બનતું હોય ત્યારે પથ તફાવત કેટલા $nm$ હશે?View Solution
- 3યંગના પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર $\frac {d}{3}$ અને પડદા વચ્ચેનું અંતર $3D$ છે. વપરાયેલ પ્રકાશની તરંગલંબાઈ $3\,\lambda$ હોય તો પડદા પર $\frac {1}{3}\,m$ માં શલાકાની સંખ્યાView Solution
- 4એક પીન હોલના કેમેરાના બોક્ષની લંબાઇ $L$ તથા તેમાં છિદ્રની ત્રિજયા $a$ છે.એમ ધારવામાં આવે છે કે જો $\lambda$ તરંગલંબાઇના સમાંતર ધારાવાળા પ્રકાશથી આ છિદ્રને પ્રકાશિત કરવામાં આવે તો સ્પોટનો વિસ્તાર ( કેમેરાની સામેની દિવાલ પર મળતા ) તેના ભૌમિતિક વિસ્તાર અને વિવર્તનના લીધેના વિસ્તારના સરવાળા જેટલો હોય.આ સ્પોટની લઘુતમ સાઝઇ ( $b_{min}$ કરો ) ત્યારે મળે કે જયારેView Solution
- 5$0.05 \,mm$ દૂર રહેલા બે બિંદુઓને $6000 \,\mathring A$ તરંગલંબાઈના પ્રકાશ વડે સૂક્ષ્મદર્શકમાં જોઈ શકાય છે. જો $3000 \,\mathring A$ તરંગલંબાઈના પ્રકાશનો ઉપયોગ કરવામા આવે તો વિભેદનની હદ .......... $mm$ થશે ?View Solution
- 6$0.1\, \mu m$ પહોળાઈ ધરાવતાં છિદ્ર (પીન હોલ) પર સૂર્ય પ્રકાશ આપાત કરતાં મળતી વિવર્તન ભાત ધ્યાનમાં લો. જે છિદ્રનો વ્યાસ થોડોક વધારીએ તો વિવર્તન ભાત પર એવી રીતે અસર થશે કે ....... .View Solution
- 7View Solutionયંગના પ્રયોગમાં જો વ્યતિકરણ કિરણોનો કંપવિસ્તાર સરખો ન હોય, તો . . . . .
- 8View Solutionનીચેનામાંથી કઈ ઘટના હાઇગેન્સના તરંગઅગ્ર રચના દ્વારા શું સમજાવી શકાતું નથી
- 9$2I _0$ જેટલી તીવ્રતા ધરાવતા એક અધ્રુવીભૂત પ્રકાશ કિરણને $P$ પોલેરોઈડમાંથી પસાર કરાવામાં આવે છે અને ત્યાર બાદ બીજા $Q$ પોલેરોઈડ કે જેની દગ અક્ષ $P$ની દગ્ અક્ષને સાપેક્ષે $30^{\circ}$ નો કોણ બનાવે તમાંથી પસાર કરવામાં આવે છે. નિર્ગમન પામતા પ્રકાશની તીવ્રતા $.......$ હશે.View Solution
- 10$I$ તીવ્રતા ધરાવતો અધ્રુવીભૂત પ્રકાશ એક આદર્શ પોલેરાઇઝર $A$ માંથી પસાર થાય છે.બીજો સમાન પોલેરાઇઝર $B$ એ $A$ ની પાછળ મૂકવામાં આવે છે. $B $ ની આગળ/પછી પ્રકાશની તીવ્રતા $\frac{I}{2}$ જેટલી માલૂમ પડ છે.હવે,બીજો સમાન પોલેરાઇઝર $C$ ને $A$ અને $B$ ની વચ્ચે મૂકવામાં આવે છે.$B$ થી આગળ તીવ્રતા $\frac{I}{8}$ જેટલી મળે છે. $A$ અને $C$ ધ્રુવીભવન ( અક્ષ ) વચ્ચેનો કોણ ________$^o$ થશે.View Solution
