બે તરંગોના કંપવિસ્તારનો ગુણોત્તર $3:5$ હોય.તો મહત્તમ અને લઘુત્તમ તીવ્રતાનો ગુણોત્તર કેટલો થાય?
Medium
Download our app for free and get started
c
(c)\(\frac{{{a_1}}}{{{a_2}}} = \frac{3}{5}\) \(\therefore \frac{{{I_{\max }}}}{{{I_{\min }}}} = \frac{{{{({a_1} + {a_2})}^2}}}{{{{({a_1} - {a_2})}^2}}} = \frac{{{{(3 + 5)}^2}}}{{{{(3 - 5)}^2}}} = \frac{{16}}{1}\)
(c)\(\frac{{{a_1}}}{{{a_2}}} = \frac{3}{5}\) \(\therefore \frac{{{I_{\max }}}}{{{I_{\min }}}} = \frac{{{{({a_1} + {a_2})}^2}}}{{{{({a_1} - {a_2})}^2}}} = \frac{{{{(3 + 5)}^2}}}{{{{(3 - 5)}^2}}} = \frac{{16}}{1}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સ્લિટ દ્વારા મળતી વિવર્તન ભાતમાં. $6000$ $A$ તરંગલંબાઈ ધરાવતા પ્રકાશનો ઉપયોગ કરવામાં આવે છે. જ્યારે પડદાને સ્લિટ થી $50 \mathrm{~cm}$ જેટલો દૂર ખસેડવામાં આવે છે ત્યારે વિવર્તન ભાતમાં પ્રથમ અને તૃતીય લધુત્તમો વચ્ચેનું અતર $3 \mathrm{~mm}$ જેટલું મળે છે. સ્લિટની પહીળાઈ_________$\times 10^{-4} \mathrm{~m}$.View Solution
- 2બે સ્લિટનો પ્રયોગ $ 500\, nm$ તરંગલંબાઈ ધરાવતા પ્રકાશ સાથે કરવામાં આવે છે. જો પાતળી તકતીની જાડાઈ $ 2\, \mu m $ અને વક્રીભવનાંક $1.5 $ હોય અને તેને સ્લીટની આગળ મૂકવામાં આવે, તો કેન્દ્રીય શલાકાનું સ્થાન .......View Solution
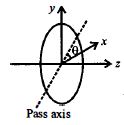
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે એક સમતલીય પોલારાઇઝર પર પ્રકાશ આપત થાય છે જેમાં તેની પાસ અક્ષ $x-$ અક્ષ સાથે $\theta$ ખૂણો બનાવે છે. $\theta$ ના ચાર અલગ મૂલ્યો , $\theta\, = 8^o, 38^o, 188^o$ અને $218^o$, માટે મળતી તીવ્રતા સમાન છે. તો ધ્રુવિભવન અને $x-$અક્ષ સાથેનો ખૂણો $^o$ માં કેટલો હશે?View Solution
- 4View Solutionનીચેનામાંથી કઈ ઘટના હાઈગેનનો સિદ્ધાંત સમજાવી શકતી નથી?
- 5એક સ્લીટને $\lambda$ જેટલી તરંગલંબાઈ ધરાવતા તરંગના પથ પર મૂકવામાં આવે છે. તો મુખ્ય મહત્તમની કોણીય પહોળાઈ ....View Solution
- 6બે સ્લિટના પ્રયોગમાં $400\,nm$ તરંગલંબાઈના પ્રકાશ માટે પડદા પર શલાકાની પહોળાઈ $2\,mm$ છે. $600\,nm$ તરંગ લંબાઈના પ્રકાશ માટે શલાકાની પહોળાઈ $..........\,mm$ થશે.View Solution
- 7યંગના બે સ્લિટના પ્રયોગમાં, મધ્યસ્થ મહતમથી $5$મી પ્રકાશિત શલાકાનું સ્થાન $5\,cm$ આગળ મળે છે. સ્લિટ અને પડદા વચ્ચેનું અંતર $1\,m$ અને વપરાયેલ એકરંગી પ્રકાશની તરંગલંબાઈ $600\,nm$ છે. સ્લિટો વચ્યેનું અંતર $............\mu m$ છે.View Solution
- 8સરખી તીવ્રતા ધરાવતા બે સુસમ્બ્ધ તરંગો મહત્તમ $100$ એકમ ઉત્પન્ન કરે છે. જો તે બન્ને ઉદ્દગમોમાંથી એકની તીવ્રતા $ 20\%$ જેટલી ઘટાડવામાં આવે તો, મહત્તમ તીવ્રતા .....View Solution
- 9$0.02\; cm$ પહોળાઇના એક રેખીય છિદ્ર $(aperture)$ ને એક $ 60 \;cm$ કેન્દ્રલંબાઇવાળા લેન્સની સામે રાખેલ છે. આ છિદ્રને $5 \times 10^{-5} \;cm $ તરંગલંબાઇવાળા લંબરૂપે આપાત પ્રકાશના સમાંતર કિરણપુંજ વડે પ્રકાશિત કરવામાં આવે છે. વિવર્તન ભાતમાં પ્રથમ અપ્રકાશિત શલાકાનું પડદાના કેન્દ્રથી અંતર ($cm$ માં) કેટલુ હશે?View Solution
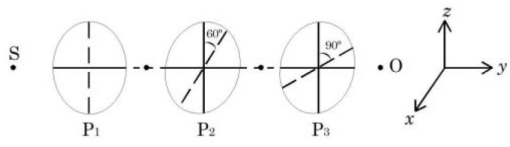
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે ત્રણ સમાન પોલેરોઈડ $P _1, P _2$ અને $P _3$ ને એક પછી એક મૂકેલા છે. $P _2$ અને $P _3$ ના અક્ષ $P _1$ ને અનુલક્ષીને અનુક્રમે $60^{\circ}$ અને $90^{\circ}$ ના કોણ પર ગોઠવેલ છે. ઉદગમ $S$ ની તીવ્રતા $O$ છે. તો $256 \;\frac{ W }{ m ^2}$ બિંદુ એ પ્રકાશની તીવ્રતા $............\frac{W}{m^2}$ છે.View Solution
