બે વર્તૂળાકાર રિંગના દળ અને ત્રિજ્યાઓના ગુણોત્તર અનુક્રમે $1 : 2$ અને $ 2 : 1$ છે. તો જડત્વની ચાકમાત્રાનો ગુણોત્તર કેટલો થશે ?
Medium
b
Here \(m_2=2 m_1\) and \(d_1=2 d_2\)
Here \(m_2=2 m_1\) and \(d_1=2 d_2\)
Moment of Tnertia of a disk \((I)=\frac{1}{2} m k^2=\frac{1}{2} m\left(\frac{d}{2}\right)^2\) ratio of moment of inertia:
\(\frac{I_1}{I_2} =\frac{1}{2} m_1\left(\frac{d_1}{2}\right)^2 / 1 / 2 m_2\left(\frac{d_2}{2}\right)^2\)
\(=\frac{m_1 d_1^2}{m_2 d_2^2}=\frac{m_1\left(2 d_2\right)^2}{\left(2 m_1\right) d_2^2}\)
\(\Rightarrow \frac{I_1}{I_2} =\frac{(2)^2}{2}=\frac{4}{2}=2\)
Hence \(I_1: I_2=2: 1\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionદઢ પદાર્થ ચાકગતિ કરે ત્યારે,તેના બધાં કણોની
- 2સમાન દળ અને ત્રિજ્યા $R$ ધરાવતી બે રીંગો ને તેમના એેક બીજા થી લંબ સમતલો સાથે અને તેમનું કેન્દ્ર એક સહિયારા બિંદુુ પર રહે તેમ મૂકવામાં આવે છે. એક રીગના સમતલને લંબ અને તેના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા શું હશે?View Solution
- 3બે તકતી જેની જડત્વની ચાકમાત્રા $I_1$ અને $I_2$ અને કોણીય વેગ $\omega_1$ અને $\omega_2$ તેમના સમતલને લંબ અને દ્રવ્યમાનકેન્દ્રમાથી પસાર થતી અક્ષ માથી પસાર થતી અક્ષને અનુલક્ષી ફરે છે.જો બંનેને એક સમાન અક્ષને અનુલક્ષીને ફરે તો તંત્રની ચાકગતિઉર્જા કેટલી થાય ?View Solution
- 4બે સરખા બોલ આકૃતિમાં દર્શાવ્યા મુજબ એક હળવા દઢ સળિયાથી જોડેલા છે. જો $J-=Mv$ એક બોલ પર લગાડવામાં આવે તો તેનો કોણીય વેગ કેટલો થાય ?View Solution

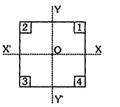
- 5આકૃતિમાં નિયમિત ચોરસ પ્લેટ દર્શાવેલી છે. જેના ખૂણા પરથી ચાર સમાન ચોરસ દૂર કરવામાં આવ્યા છે.ચોરસ $-1$ ને દૂર કરતાં $ C.M.$ ક્યાં મળશે ?View Solution
- 6View Solutionતંત્રને સમતોલન સ્થિતિમાં રાખવા માટે તેના પર લાગતા ટોર્કને સંતુલિત કરવું પડે . આ વિધાન સાચું કરવા માટે ટોર્ક ક્યાં લેવું પડે ?
- 7View Solutionઘર્ષણ રહિત ઢાળની સપાટીના ઉપરના છેડેથી એક નક્કર ગોળો, પોલો ગોળો અને રિંગને મુક્ત કરવામાં આવે છે. જેથી તેઓ ઢાળ પર સરકે છે. ઢાળના તળિયે કયા પદાર્થનો રેખીય પ્રવેગ મહત્તમ હશે ? પદાર્થ ઢાળ પર ગબડતા નથી.
- 8ટોર્ક મેળવવા માટે ઇલેકટ્રીક મોટરની ધરીનેે સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કરવામાં આવે છે. તે $\alpha = 3t - t^2$, જેટલું કોણીય પ્રવેગ પ્રાપ્ત કરે છે. તેની ચાકગતિની શરૂઆત થયાના $2\ seconds $ બાદ $\alpha = 0. $ થાય, તો $6\ seconds$ પછી તેનો કોણીય વેગ ગણો.View Solution
- 9બે રિંગની જડત્વની ચાકમાત્રા $4 : 1$ ના ગુણોત્તરમાં છે. અને તેમના વ્યાસ $ 4 : 1$ ના ગુણોત્તરમાં છે. તો તેમના દળના ગુણોત્તર શોધો.View Solution
- 10$2L $ લંબાઈનો સમાન સળીયાનો એક છેડો સમક્ષીતિજ સાથે સંપર્કમાં છે તથા બીજા છેડાને સમક્ષીતીજ સાથે $\alpha$ કોણ બનાવીને સંપર્ક આગળ સરકે નહીં તે રીતે છોડવામાં આવે તો સમક્ષીતિજ આવે ત્યારે તેનો કોણીય વેગ કેટલો હશે ?View Solution
