બંધ પાત્રમાં $2N_2O_5(g) $ $\rightleftharpoons$ $ 4NO_2(g) + O_2(g)$ નો અભ્યાસ કરતાં $NO_2$ ની સાંદ્રતા પાંચ સેકન્ડમાં $2.0 × 10^{-2} mol L^{-1}$ વધે છે. તો $N_2O_5$ ની સાંદ્રતા ફેરફારનો દર ગણો.
Medium
Download our app for free and get started
c
\({N_2}{O_5}\) ની સાંદ્રતા ના ફેરફારનો દર \( = \,\,{\text{ - }}\frac{{{\text{d[}}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{]}}}}{{{\text{dt}}}}\,\, = \,\,{\text{ - }}\frac{{\text{1}}}{{\text{2}}}\,\,\,{\text{N}}{{\text{O}}_{\text{2}}}\,\)
\({N_2}{O_5}\) ની સાંદ્રતા ના ફેરફારનો દર \( = \,\,{\text{ - }}\frac{{{\text{d[}}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{]}}}}{{{\text{dt}}}}\,\, = \,\,{\text{ - }}\frac{{\text{1}}}{{\text{2}}}\,\,\,{\text{N}}{{\text{O}}_{\text{2}}}\,\)
નું નિર્માણ દર \( = \,\, - \frac{{\text{1}}}{{\text{2}}}\,\frac{{d[N{O_2}]}}{{dt}}\,\, = \,\, - \frac{1}{2}\,\, \times \,\,4\,\, \times \,\,{10^{ - 3}}\,\, = \,\,2\,\, \times \,\,{10^{ - 3}}\,mol\,\,{L^{ - 1}}\,{s^{ - 1}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉષ્માશોષક પ્રક્રિયા માટે, જ્યાં $\Delta H$ $kJ/mol$માં પ્રક્રિયાના એન્થાલ્પીનું પ્રતિનિધિત્વ કરે છે, સક્રિયકરણની ઊર્જા માટે ન્યૂનતમ મૂલ્ય શું હશે?View Solution
- 2તાપમાન સાથે પ્રક્રિયાનો વેગ અચળાંક નીચેના સમીકરણ મુજબ બદલાય છે. $\log \,K = $ constant $ - {E_a}/2.303\,RT$ જો $\log \,K \to 1/T$ નો આલેખ $- 5632$ જેટલો ઢાળ ધરાવતી સીધી રેખા મળે, તો પ્રક્યિાની સક્રિયકરણ ઊર્જા .......... $kJ\, mol^{-1}$ મળશે.View Solution
- 3નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.View Solution
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
સ્ટેપ Rate constant $\left(\sec ^{-1}\right)$
Activation energy
$\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
$1$ ${k}_1$ $300$ $2$ ${k}_2$ $200$ $3$ ${k}_3$ $\mathrm{Ea}_3$ ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).
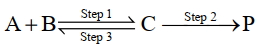
- 4$A\rightarrow$ નિપજ ચોક્કસ પ્રક્રિયાનો અર્ધઆયુ સમય $1$ કલાક છે. જ્યારે પ્રક્રિયક $ 'A' $ ની શરૂઆતની સાંદ્રતા $2.0$ મોલ $L^{-1}$ હોય તો જો શૂન્ય ક્રમની પ્રક્રિયા હોય તો તેની સાંદ્રતા $0.50$ થી $0.25$ મોલ $L^{-1}$ સુધી આવતાં ......... $h$ લેશે.View Solution
- 5એક પ્રથમ ક્રમની પ્રક્રિયા માટે વેગ અચળાંક $4.606 \times 10^{-3} s ^{-1} $. પ્રક્રિયાનાં $2.0\, g$ માંથી $0.2\, g$માં થતાં ઘટાડા માટે ......... $s$ સમય જરૂરી છે?View Solution
- 6ફ્લાસ્કમાં સંયોજનોનું $A$ અને $B$ મિશ્રણ હોય છે બંને સંયોજન પ્રથમ ક્રમથી વિઘટન પામે છે તેની અર્ધ આયુષ્યસમય $A$ અને $B$ નું અનુક્રમે $300$ $s$અને $180\, s ,$છે જો $A$ અને $B$ ની સાંદ્રતા આંશિક સમાન હોય $ A $ ની સાંદ્રતા માટે સમય $B$ કરતા ચાર ગણો કેટલો સમય જરૂરી છેView Solution
- 7$2A + B \rightarrow 3C + D$ પ્રક્રિયા માટે નીચેનામાંથી કયું એક પ્રક્રિયા દર આપતો નથી?View Solution
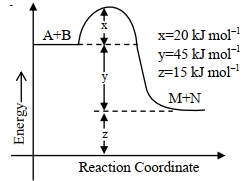
- 8નીચેના આંકડા મુજબ, પ્રક્રિયાના એન્થાલ્પી ફેરફારની તીવ્રતાView Solution
${A}+{B} \rightarrow {M}+{N}$ $......$ ${kJ} {mol}^{-1}$ બરાબર છે. (નજીકના પૂર્ણાંકમાં)
- 9$N_2O_5\rightarrow 2NO_2 + \frac{1}{2} O_2$ પ્રથક્રમની પ્રક્રિયા છે. તેનો અર્ધ આયુષ્યસમય $2.4 $ કલાક $STD$ એ છે. પ્રક્રિયાની શરૂઆતમાં $10.8 \,gm \,N_2O_5 $ લેવામાં આવે તો $9.6$ કલાક બાદ ........ લિટર ઓક્સિજન પ્રાપ્ત થશે.View Solution
- 10નીચેનો પ્રક્રિયા $A+ B\to C$ માટે બતાવેલ ડેટાને અનુરૂપ વેગ નિયમ પસંદ કરોView Solution
Expt. No. $(A)$ $(B)$ પ્રારંભિક દર $1$ $0.012$ $0.035$ $0.10$ $2$ $0.024$ $0.070$ $0.80$ $3$ $0.024$
$0.035$ $0.10$ $4$ $0.012$ $0.070$ $0.80$