(c)
\(K _{\text {Rother }}= K _{\text {Trenstation }}+ K _{\text {rotaton }}\)
\(=\frac{1}{2} m v^2+\frac{1}{2} l \omega^2\)
\(=\frac{1}{2} m R^2 \omega^2+\frac{1}{2}\left|\omega^2=\frac{1}{2}\right| \omega^2\left(1+\frac{m R^2}{1}\right)\)
\(\Rightarrow\) ratio \(=\frac{K_{\text {waton }}}{K_{\text {total }}}=\frac{\frac{1}{2} I ^2}{\frac{1}{2} I_{\omega^2}\left(1+\frac{m R^2}{1}\right)}\)
\(=\frac{1}{1+\frac{m R^2}{1}}\)
For disc,
\(\text { Ratio }=\frac{1}{1+\frac{m R^2}{\left(\frac{m R^2}{2}\right)}}=\frac{1}{3}\)
Solid sphere
\(\text { Ratio }=\frac{1}{1+\frac{m R^2}{\frac{2}{5} m R^2}}=\frac{2}{7}\)
Ring
\(\text { Ratio }=\frac{1}{1+\frac{m R^2}{m R^2}}=\frac{1}{2}\)
Hollow sphere ratio \(=\frac{1}{1+\frac{m R^2}{\frac{2}{3} m R^2}}=\frac{2}{5}\)
Hence \(ring\) correct option.
Download our appand get started for free
Similar Questions
- 1એક $M$ દળ અને $R$ ત્રિજયાની પાતળી વર્તુળાકાર પ્લેટની ઘનતા $p\left( r \right) = {p_0}\,r$ મુજબ બદલાય છે જ્યાં $P_0$ અચળાંક અને $r$ કેન્દ્રથી અંતર છે.વર્તુળાકાર પ્લેટને લંબ અને તેની ધારમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I = aMR^2$ હોય તો $a$ કેટલું થાય?View Solution
- 2View Solutionતરવૈયો પાણીમાં જતાં પહેલાં પોતાના શરીરને સંકોચે છે, જેથી......
- 3View Solutionએક કીડી ચાકગતિ કરતી તકતીની કિનારી પર બેઠેલી છે. જો કીડી વ્યાસ પરથી ચાલીને બીજા છેડે પહોંચે ત્યારે તકતીનો કોણીય વેગ કેટલો હશે?
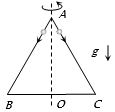
- 4View Solutionસમબાજુની બાજુ પર બે રિંગ સરકે છે. તો નીચેનામાંથી કયા જોડનું સંરક્ષણ થશે?
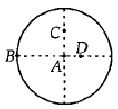
- 5View Solutionનિયમિત વર્તુળાકાર તકતીના સમતલને લંબ કયાં બિંદુમાંથી પસાર થતી કઇ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા મહત્તમ થાય?
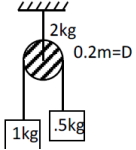
- 6આકૃતિમાં દર્શાવેલ $0.2\, m$ વ્યાસ અને $2\, kg$ દળ ધરાવતી પુલી પર રહેલ $1\, kg$ દળના પદાર્થનો પ્રવેગ ($m / s ^{2}$ માં) કેટલો હશે?View Solution
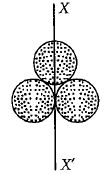
- 7આકૃતિમાં દર્શાવ્યા અનુસાર, દરેક $m$ દળના અને $r $ ત્રિજયા ધરાવતા ત્રણ સમાન પોલા ગોળાઓ પડેલા છે. તેમાંના કોઇ બે ગોળાને સ્પર્શતા અને ત્રીજા ગોળાના વ્યાસરૂપે રહેલી અક્ષ $XX’$ વિચારો. ત્રણ ગોળાઓથી બનેલા તંત્રની $XX’ $ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 8$2\ kg $ દળ ધરાવતો એક દઢ પદાર્થ $ 0.8\ m$ ત્રિજ્યા ધરાવતા, એક વર્તૂળાકાર પથ પર $44 \ rad s^{-1 }$ ના કોણીય વેગથી ગતિ કરે છે. જો આ વર્તૂળાકાર પથની ત્રિજ્યા $1 \ m $ થાય, તો આ પદાર્થનો નવો કોણીય વેગ ........ $rad\, s^{-1}$ થાય.View Solution
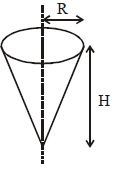
- 9આકૃતિમાં પોલો આઇસ્ક્રીમ કોન છે ,તેનું દળ $M,$ ઉપરની ત્રિજ્યા $R$ અને ઊંચાઈ $H$ છે,તો આપેલી અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા ......View Solution
- 10જે પદાર્થનો કોણીય વેગમાન $200\%$ વધારવામાં આવે તો તેની ચાકગતિઊર્જામાં ........ $\%$ વધારો થશે.View Solution
