એક $M$ દળ અને $R$ ત્રિજયાની પાતળી વર્તુળાકાર પ્લેટની ઘનતા $p\left( r \right) = {p_0}\,r$ મુજબ બદલાય છે જ્યાં $P_0$ અચળાંક અને $r$ કેન્દ્રથી અંતર છે.વર્તુળાકાર પ્લેટને લંબ અને તેની ધારમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I = aMR^2$ હોય તો $a$ કેટલું થાય?
JEE MAIN 2019, Diffcult
a
\(M = \int\limits_0^R {{\rho _0}r\left( {2\pi rdr} \right) = \frac{{{\rho _0} \times 2\pi \times {R^3}}}{3}} \)
\(M = \int\limits_0^R {{\rho _0}r\left( {2\pi rdr} \right) = \frac{{{\rho _0} \times 2\pi \times {R^3}}}{3}} \)
\(\,\,\,\mathop {{I_0}}\limits_{\left( {MOl\,about\,COM} \right)} = \int\limits_0^R {{\rho _0}r} \left( {2\pi rdr} \right) \times {r^2} = \frac{{{\rho _0} \times 2\pi {R^5}}}{5}\)
By parallel axis theorem
\(I = {I_0} + M{R^2}\)
\( = \frac{{{\rho _0} \times 2\pi {R^5}}}{5} + \frac{{{\rho _0} \times 2\pi {R^3}}}{3} \times {R^2} = {\rho _0}2\pi {R^5} \times \frac{8}{{15}}\)
\( = M{R^2} \times \frac{8}{5}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$5\,kg$નું એક બાળક ચકડોળમાં ફરે છે જે $3.14\,s$ માં $1$ પરિભ્રમણ પૂર્ણ કરે છે. ચકડોળની ત્રિજ્યા $2\,m$ છે. બાળક પર લાગતું કેન્દ્રત્યાગી બળ $.......\,N$ હશેView Solution
- 2ચાર સળિયાઓને ચોરસના સ્વરૂપે મૂકેલા છે. સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા ગણો. ( દળ $ M$ અને લંબાઈ $ L$ )View Solution
- 3$'r'$ ત્રિજ્યા ધરાવતા પૈડાના પરીઘનાં ફરતે દોરી વિટાળવામાં આવે છે. પૈડાની અક્ષ સમક્ષીતીજ તેમજ તે અક્ષને અનુલક્ષિને જડત્વની ચાકમાત્રા $I$ છે. દોરીના છેડે $mg$ વજન લટકાવવામાં આવે છે. વજન વિરામ સ્થિતિમાંથી પતન કરે છે.$‘h'$ ઊંચાઈ પરથી પતન પછી, પૈડાના કોણીય વેગનો વર્ગ ...... હશે.View Solution
- 4$m$ દળનાં એક બોમ્બને જમીન પરથી $v$ ઝડપે સમક્ષિતિજ સાથે $\theta$ ખૂણાથી પ્રક્ષેપિત કરવામાં આવે છે. જમીન થી મહત્તમ ઊંચાઈએ થી તે બોમ્બ બે સમાન દળના ટુકડાઓ માં વિસ્ફોટ પામે છે. જો એક ટુકડો વિસ્ફોટ બાદ તરત જ સ્થિર સ્થિતિમાં આવતો હોય, તો દ્રવ્યમાન કેન્દ્રની સમક્ષિતિજ અવધિ શું હશે ?View Solution
- 5$P$ અને $ Q $ રીંગને એકસમાન તારમાંથી બનાવવામાં આવે છે.તેમની ત્રિજયા $r_1$ અને $r_2$ છે.તેની જડત્વની ચાકમાત્રા $I_1$ અને $I_2$ છે.જો $I_2/I_1 =4$ હોય,તો $r_2\over r_1$ =View Solution
- 6$30\, cm$ લંબાઇના એક પોલા નળાકારની (અંદરની ત્રિજ્યા $10\, cm$ અને બહારની ત્રિજ્યા $20 \,cm$) તેના અક્ષની સાપેક્ષે જડત્વની ચાકમાત્રા $I$ છે. આવું સમાન દ્રવ્યમાન ધરાવતા એક પાતળા નળાકારની તેના અક્ષની સાપેક્ષે જડત્વની ચાકમાત્રા પણ $I$ છે, તો તેની ત્રિજ્યા ........ $cm$ હશેView Solution
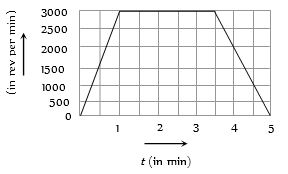
- 7View Solutionએક પ્રયોગમાં એક જેટ એંજિનનું કમ્પ્રેસર નીચે આપેલા ગ્રાફ પ્રમાણે ફરે છે તો પ્રયોગ દરમિયાન કમ્પ્રેસરના પરિભ્રમણ સંખ્યા કેટલી હોય ?
- 8View Solutionસુરેખ સપાટી પર કોઈ તકતી સરક્યાં વગર ગબડે છે. તો રેખીય ગતિઉર્જા નો કુલ ગતિઉર્જા સાથેનો ગુણોત્તર શું મળે?
- 9એક ધરી પર રહેલ પૈડાની જડત્વની ચાકમાત્રા $3 \times 10^2\ kg m^2$ છે તથા અચળ કોણીય ઝડપ $4.6\ rad\ s^{-1}$ છે. જો પૈડા પર લાગતું પ્રતિટોર્ક $6.9\times10^2\ N.m $ હોય તો ...... (સેકન્ડ) સમયમાં પૈડુ ઉભું રહી જાય ?View Solution
- 10$R$ ત્રિજયા અને $M$ દળ ધરાવતી એક નિયમિત વર્તુળાકાર તકતીને લંબ એવી રીતે તેની ધારમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
