ચક્રિય પ્રતિવર્તી એન્જિન માટે તાપમાન વિરુધ્ધ એન્ટ્રોપીનો ગ્રાફ આપેલ છે તો એન્જિનની કાર્યક્ષમતા કેટલી હશે?
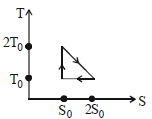
AIIMS 2008, Diffcult
Download our app for free and get started
d
\(\mathrm{Q}_{1}=\mathrm{T}_{0} \mathrm{S}_{0}+\frac{1}{2} \mathrm{T}_{0} \mathrm{S}_{0}=\frac{3}{2} \mathrm{T}_{0} \mathrm{S}_{0}\)
\(\mathrm{Q}_{1}=\mathrm{T}_{0} \mathrm{S}_{0}+\frac{1}{2} \mathrm{T}_{0} \mathrm{S}_{0}=\frac{3}{2} \mathrm{T}_{0} \mathrm{S}_{0}\)
\({\mathrm{Q}_{2}=\mathrm{T}_{0}\left(2 \mathrm{S}_{0}-\mathrm{S}_{0}\right)=\mathrm{T}_{0} \mathrm{S}_{0} \text { and } \mathrm{Q}_{3}=0}\)
\({\eta=\frac{\mathrm{W}}{\mathrm{Q}_{1}}=\frac{\mathrm{Q}_{1}-\mathrm{Q}_{2}}{\mathrm{Q}_{1}}} \)
\({=1-\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}}=1-\frac{\mathrm{T}_{0} \mathrm{S}_{0}}{\frac{3}{2} \mathrm{T}_{0} \mathrm{S}_{0}}=\frac{1}{3}}\)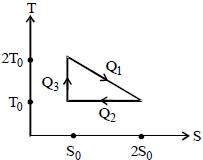
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કાર્નોટ એન્જિન $T$ તાપમાને રહેલ ઉષ્માપ્રાપ્તિ સ્થાનમાંથી $Q$ ઉષ્મા મેળવે છે.તેમાંથી કેટલી ઉષ્મા $T/3$ તાપમાને રહેલ ઠારણ વ્યવસ્થામાં મુકત કરશે?View Solution
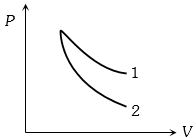
- 2બે વાયુના સમોષ્મી પ્રક્રિયાના ગ્રાફ આપેલા છે.તો ગ્રાફ $1$ અને $2$ કયાં વાયુના હશે.View Solution
- 3$30 °C$ અને $0 °C$ તાપમાન વચ્ચે કાર્ય કરતા કાર્નોટ રેફ્રિજરેટરનો પરફોર્મન્સ ગુણાંક ......View Solution
- 4કોઈ ચોક્કસ થર્મોડાયનેમિક પ્રક્રિયામાં, વાયુનું દબાણ તેના પ્રારંભિક કદ પર $kV^3$ જેટલો આધાર રાખે છે. જ્યારે તાપમાન $100^{\circ} C$ થી $300^{\circ} C$ બદલવામાં આવે છે ત્યારે થતું કાર્ય ............$nR$ થશે, જ્યાં $n$ એ વાયુ માટે મોલ સંખ્યા દર્શાવે છે.View Solution
- 5જો ઠારણ વ્યવસ્થાનું તાપમાન નિરપેક્ષ શૂન્ય પર છે, તો કાર્નોટ એન્જિનની કાર્યક્ષમતા ......... $\%$ થશે.View Solution
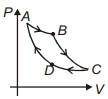
- 6કાર્નોટ ચક્ર $P-V$ આલેખમાં દોરેલ છે. ક્યો ભાગ સમતાપી પ્રસરણ રજૂ કરે છે ?View Solution
- 7View Solutionપુનઃસંયોજનનું મુલ્ય ક્યાં નીયમનાં આધાર પર હોય છે ?
- 8View Solutionવાયુની આંતરિક ઊર્જા કોના પર આધારિત છે?
- 9એક રેફ્રિજરેટરનું અંદરનું તાપમાન $t_2\, ^o C$ છે અને ઓરડાનું તાપમાન $t_1 \,^o C$ છે. આદર્શ અવસ્થામાં પ્રતિજૂલ વિદ્યુતઊર્જાનો વ્યય થાય ત્યારે, ઓરડાને આપેલી ઉષ્માનું મૂલ્ય કેટલું હશે?View Solution
- 10આદર્શવાયુના એક પ્રયોગ દરમિયાન તે વાયુ એક વધારાના નિયમ $VP^2$ અચળનું પાલન કરતાં જણાય છે. તેનું પ્રારંભિક તાપમાન $T$ અને કદ $V$ છે. જે તેનું કદ વધારીને $2 V$ થાય. ત્યારે અંતિમ તાપમાન કેટલું થશે?View Solution