$CO_2$ અને $H_2O$ ની નિર્માણ ઉષ્મા અનુક્રમે $-97 \,kcal$ અને $-68\, kcal $ છે. બેન્ઝિનની દહન ઉષ્મા $-783 \,kcal$ છે. તો બેન્ઝિનની નિર્માણ ઉષ્મા કેટલા .......$kcal$ ?
Diffcult
Download our app for free and get started
a
આપેલ છે :
આપેલ છે :
\((i)\) : \(C_6H_{6(l)} + \frac{15}{2} O_{2(g)}\) \(→\) \(6CO_{2(g)} + 3H_2O_{(l)}\)
\(\Delta H\) = \(-783\,K\,cal\)
\((ii)\) : \(C_{(s)} + O_{2(g)}\) \(→\) \(CO_{2(g)}\)
\(\Delta H\) = \(-97\,K\,cal\)
\((iii)\) : \(H_{2(g)} + \frac{1}{2} O_{2(g)}\) \(→\) \(H_2O_{(g)}\)
\(\Delta H\) = \(-68\,K\,cal\)
જેથી,
\(6CO_{2(g)} + 3H_2O_{(l)}\) \(→\) \(C_6H_{6(l)} + \frac{15}{2} O_{2(g)}\)
\(\Delta H\) = \(+783\,K\,cal\)
\(6C_{(s)} + 6O_{2(g)}\) \(→\) \(6CO_{2(g)}\)
\(\Delta H\) = \(-582\,K\,cal\)
\(3H_{2(g)} + \frac{3}{2} O_{2(g)}\) \(→\) \(3H_2O_{(g)}\)
\(\Delta H\) = \(-204\,K\,cal\)
ઉમેરવાથી,
\(6C_{(s)} + 3H_{2(g)}\) \(→\) \(C_6H_{6(l)}\)
\(\Delta H = -3\,K\,cal\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપ્રવાહીનું બાષ્પીભવન માટેની પ્રક્રિયા ....... થઈ પૂર્ણ થાય છે.
- 2$CaC_2$ ઉત્પન્ન કરવા $233.0\, g$ કેલ્શિયમ ઓક્સાઇડની પૂરતા પ્રમાણમાં કાર્બન સાથે પ્રકિયા થતા કેટલા .....$kJ$ ઉષ્માનો ફેરફાર થશે ?$Ca{O_{\left( s \right)}} + 3{C_{\left( s \right)}} \to Ca{C_{2\left( g \right)}} + C{O_{\left( g \right)}}\,\,;\,\Delta {H^o} = 464.8\,kJ/mol$View Solution
- 3સ્પ્રિંગના સંકોચન દરમિયાન $10\,kJ$ કાર્ય થાય છે અને $2\,kJ$ ઉષ્મા તરીકે પર્યાવરણમાં મુક્ત થાય છે. તો આંતરિક ઊર્જામાં થતો ફેરફાર $\Delta U$ ($kJ$ માં) જણાવો.View Solution
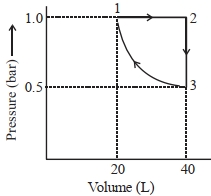
- 4એક મોલ આદર્શ એકપરમાણ્વીય વાયુને આલેખમાં દર્શાવ્યા પ્રમાણે ફેરફાર કરેલ છે. થયેલ કાર્યની માત્રા (પ્રણાલી વડે અથવા પ્રણાલી ઉપર) $..........J$ છે. (નજીકનો પૂર્ણાક) Given : $\log 2=0.3, \ln 10=2.3$View Solution
- 5નીચેના પ્રકમો પરથી પ્રકિયા $B + D \rightarrow E + 2C$ માટે $\Delta H$ નું મૂલ્ય કેટલા ........... $\mathrm{kJ/mol}$ હશે તે જણાવો.View Solution
$\Delta H \,(kJ/mol)$ $\frac 12 A \rightarrow B$ $+150$ $3B \rightarrow 2C + D$ $-125$ $E + A \rightarrow 2D$ $+350$ - 6નીચે આપેલી પ્રક્રિયા $298 \,K$ તાપમાને કરવામાં આવી.View Solution
$2NO(g) + O_2(g) \rightleftharpoons 2NO_2(g)$
$298 \,K$ તાપમાને $NO(g)$ ની પ્રમાણિત સર્જન મુક્તઊર્જા $86.6\, kJ/mol$ છે. તો $298 \,K.$ તાપમાને $NO_2(g)$ ની પ્રમાણિત સર્જન મુક્તઊર્જા કેટલી થશે ? ($K_p = 1.6 \times 10^{12})$
- 7View Solutionપ્રવાહીનું બાષ્પીભવન માટેની પ્રક્રિયા ....... થઈ પૂર્ણ થાય છે.
- 8View Solutionગેલ્વેનિક કોષમાં થતું કાર્ય એ કોના બરાબર થાય છે?
- 9સિલિન્ડરમાં $1$ વાતા. અચળ દબાણે $1.2$ લીટર $O_2$ વાયુમાં $1.0$ કિલો કેલરી ઉષ્મા ઉમેરવામાં આવે છે અને કદમાં $1.5$ લીટર ફેરફાર થાય છે. તો આ પ્રક્રિયામાં થતો આંતરિક ઊર્જાનો ફેરફારની ગણતરી ..... થશે.View Solution
- 10View Solutionઉષ્માગતિશાસ્ત્ર....... સાથે સંપર્ક ધરાવે છે.