ડબલ સ્લિટના એક પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર $19.44\, \mu m$ અને તેની પહોળાઈ $4.05\, \mu m$ છે જેના પર લીલા $\left( {5303\,\mathop A\limits^o } \right)$ પ્રકાશને આપાત કરવામાં આવે છે. પ્રથમ અને દ્વિતીય વ્યતિકરણ ન્યૂનતમ વચ્ચે રહેલ પ્રકાશિત શલાકાઓની સંખ્યા કેટલી હશે?
JEE MAIN 2019, Diffcult
b
For diffraction
For diffraction
Location of \(1^{\text {st }}\) minima
\({y_1} = \frac{{D\lambda }}{a} = 0.2469\,D\lambda \)
Location of \(2^{\text {nd }}\) minima
\({{\text{y}}_2} = \frac{{2{\text{D}}\lambda }}{{\text{a}}} = 0.4938\,{\text{D}}\lambda \)
Now for interference
Path for interference
Path difference at \(P\)
\(\frac{d y}{D}=4.8 \lambda\)
Path difference at \(P\)
\(\frac{d y}{D}=9.6 \lambda\)
So orders of maxima in between \(\mathrm{P}\) and \(\mathrm{Q}\) is
\(5,\,6,\,7,\,8,\,9\)
So \(5\) bright fringes all present between \(\mathrm{P}\) and \(\mathrm{Q}\)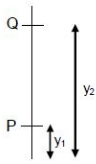
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સ્લીટ વિવર્તનમાં પ્રથમ વિવર્તન ન્યૂનતમ $\theta = {30^o}$ ના ખૂણે મળે છે જેમાં $5000\,\mathop A\limits^o $ તરંગલંબાઈ સ્લીટને લંબ આપત થાય છે. તો સ્લીટની પહોળાઈ કેટલી હશે?View Solution
- 2View Solutionદ્રવ્યનો વક્રીભવનાંક એ ધ્રુવીભુત કોણના બરાબર હોય છે. તેને .....
- 3View Solutionવિવર્તનને જોવા માટે દર્પણ મુખનું પરિમાણ . . . . . .
- 4માઇક્રોસ્કોપમાં રહેલ વસ્તુકાંચનો વ્યાસ મુખ્યકેન્દ્ર સાથે $\beta $ ખૂણો બનાવે છે. વસ્તુ અને લેન્સ વચ્ચેનું માધ્યમ તેલ છે જેનો વક્રીભવનાંક $n$ છે. તો માઇક્રોસ્કોપનો વિભેદન પાવર ....View Solution
- 5યંગના પ્રયોગમાં પડદા પરના જે બિંદુએ પથ-તફાવત $\lambda/6$ છે ત્યાં તીવ્રતા $I$ છે. જો મધ્યસ્થ પ્રકાશિત શલાકાની તીવ્રતા $I_0$ હોય, તો $I/I_0$ = …View Solution
- 6યંગના બે સ્લિટના પ્રયોગમાં મધ્યસ્થ અધિકતમની તીવ્રતા $I_0 $ છે. બંને સ્લિટો વચ્ચેનું અંતર $d=5\lambda$ છે, જયાં $\lambda$ એ પ્રયોગમાં વપરાયેલ પ્રકાશની તરંગલંબાઇ છે. કોઈ એક સ્લિટની સામે $D=10d$ અંતરે આવેલા પડદા પર તીવ્રતા કેટલી હશે?View Solution
- 7યંગના પ્રયોગમાં બે સ્લિટ વ્ચ્ચેનું અંતર $1\,mm$ અને સ્લિટ પડદા વચ્ચેનું અંતર $100\,cm$ છે વપરાયેલ પ્રકાશની તરંગલંબાઈ $632.8\,nm$ છે મધ્યસ્થ પ્રકાશિત શલાકાથી $1.27\,mm$ અંતરે પ્રકાશિત શલાકા મળતી હોય તો તે બિંદુ આગળ સ્લિટ માંથી આવતા તરંગો વચ્ચે પથ તફાવત $....\mu m$View Solution
- 8$10\; cm$ વસ્તુકાંચનો વ્યાસ ધરાવતા ટેલિસ્કોપને બે વસ્તુથી એક કિલોમીટર અંતરે મુકેલ છે. આવતા પ્રકાશની સરેરાશ તરંગલંબાઈ $5000 \;\mathring A$ હોય, તો આ વસ્તુને અલગ અલગ જોવા માટે તેમની વચ્ચેનું અંતર કયા ક્રમનું હશે?View Solution
- 9યંગના ડબલ સ્લીટના પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર સમય સાથે ${d}({t})={d}_{0}+{a}_{0}\, sin\omega \,t$ મુજબ બદલાય છે; જ્યાં ${d}_{0}, \omega$ અને $a_{0}$ અચળાંકો છે. સ્થિર છે. સમય સાથે મેળવેલી સૌથી મોટી શલાકાની પહોળાઈ અને સૌથી નાની શલાકાની પહોળાઈ વચ્ચેનો તફાવત કઈ રીતે આપવામાં આવે?View Solution
- 10View Solutionફેશનલના બાયપ્રિઝમમાં સુસંબદ્ધ તરંગો ...... દ્ધારા મેળવવામાં આવે છે.
