યંગના બે સ્લિટના પ્રયોગમાં મધ્યસ્થ અધિકતમની તીવ્રતા $I_0 $ છે. બંને સ્લિટો વચ્ચેનું અંતર $d=5\lambda$ છે, જયાં $\lambda$ એ પ્રયોગમાં વપરાયેલ પ્રકાશની તરંગલંબાઇ છે. કોઈ એક સ્લિટની સામે $D=10d$ અંતરે આવેલા પડદા પર તીવ્રતા કેટલી હશે?
NEET 2016, Diffcult
c
Here, \(d=5 \lambda\), \(D=10\,d\), \(y=\frac{d}{2}\) .
Here, \(d=5 \lambda\), \(D=10\,d\), \(y=\frac{d}{2}\) .
Resultant Intensity at \(y=\frac{d}{2}, I_{y}=?\)
The path difference between two waves at \(y=\frac{d}{2}\)
\(\Delta x = d\tan \theta = \) \(d \times \frac{y}{D} = \) \(\frac{{d \times \frac{d}{2}}}{{10d}} = \) \(\frac{d}{{20}} = \frac{{5\lambda }}{{20}} = \frac{\lambda }{4}\)
Corresponding phase difference, \(\phi=\frac{2 \pi}{\lambda} \Delta x=\frac{\pi}{2}\)
Now, maximum intensity in Young's double slit experiment,
\({I_{\max }} = {I_1} + {I_2} + 2{I_1}{I_2}\)
\({I_0} = 4I\) \((\because \,\,{I_1}\, = \,{I_2}\, = \,I)\)
\(\therefore I=\frac{I_{0}}{4}\)
Required intensity,
\({I_y} = {I_1} + {I_2} + 2{I_1}{I_2}\cos \frac{\pi }{2}\) \( = 2I = \frac{{{I_0}}}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1યંગના ડબલ સ્લિટના બે અલગ અલગ પ્રયોગમાં શલાકાની પહોળાઇ સમાન છે,વપરાયેલ પ્રકાશની તરંગલંબાઇનો ગુણોત્તર $1:2$ અને સ્લિટની પહોળાઇનો ગુણોત્તર $2:1$ છે,તો સ્લિટ અને પડદા વચ્ચેના અંતરનો ગુણોત્તર કેટલો થાય?View Solution
- 2એક સ્લીટ વિવર્તનમાં પ્રથમ વિવર્તન ન્યૂનતમ $\theta = {30^o}$ ના ખૂણે મળે છે જેમાં $5000\,\mathop A\limits^o $ તરંગલંબાઈ સ્લીટને લંબ આપત થાય છે. તો સ્લીટની પહોળાઈ કેટલી હશે?View Solution
- 3પ્રારંભમાં માઈક્રોસ્કીપનો ઓબજેકિટવ (લેન્સ) હવામાં (વક્રીભવનાંક $1$) અને હવે તેલ (વક્રીભવનાંક $2$)માં ડૂબાડવામાં આવેલ છે. જેની હવામાં તરંગલંબાઈ $\lambda$ હોય તેવા અચળ પ્રકાશ માટે તેલમાં માઈક્રોસ્કોપની વિભેદન શક્તિમાં થતો ફરફાર ગણો.View Solution
- 4$50\,cm$ પહોળાઈ ધરાવતી નદીના કિનારા પર બહુમાળી ઈમાતરત છે દીવાદાંડીના ટાવરની ઊંચાઈ $40\,m$ છે $10\,m$ ઊંચાઈથી માણસને દીવાદાંડી નો પ્રકાશ પાણીની સપાટીથી ધ્રુવીભૂત થઈને દેખાય છે તે ઇમારતથી $x$ અંતરે થી આવતો પ્રકાશની તીવ્રતા લઘુતમ છે તે દીવાદાંડી પર રહેલા $y$ ઊંચાઈના બ્લબમાંથી આવતા પ્રકાશની તીવ્રતા બરાબર છે તો $x$ અને $y$ ના મૂલ્યો (પાણીનો વક્રીભવનાંક $ \simeq \frac{4}{3})$) છે.View Solution
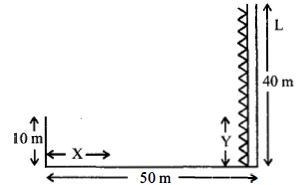
- 5View Solutionકેવા ઉદ્ગમમાંથી ઉત્સર્જાતા તરંગો સુસબંદ્વ હોય ?
- 6View Solutionહાઇગેન્સની થીયરીમાં તરંગઅગ્રથી...
- 7પોલારાઇઝરમાંથી પસાર થયા પછી, $I$ તીવ્રતાનો એક રેખીય ધ્રુવીભૂત પ્રકાશ એ પોલરાઇઝર સાથે $30^{\circ}$નો ખૂણો બનાવતા એનાલાઈઝર પર પડે છે. એનાલાઈઝરમાંથી ઉત્સર્જિત પ્રકાશની તીવ્રતા કેટલી હશે?View Solution
- 8View Solutionયંગના બે સ્લિટના પ્રયોગમાં એકરંગી પ્રકાશ ના સ્થાને સફેદ પ્રકાશ લેવામાં આવે તો......
- 9યંગના પ્રકાશના વ્યતિકરણના પ્રયોગમાં પાળી પ્રકાશ ($\lambda 5896 \,A$ ) થી પ્રકાશિત કરેલ સ્લીટો $0.2 \,cm$ ની છે. સ્લીટના સમતલથી $1 m$ અંતરે રાખેલા પડદા પર મળતી શલાકાની પહોળાઈ કેટલી હશે. જો તંત્રને પાણીમાં ડુબાડેલું હશે તો શલાકાની પહોળાઈ કેટલી હશે?View Solution
- 10View Solutionતારા પૃથ્વી તરફ ગતિ કરે ત્યારે પ્રકાશનું શિફ્ટ
