ધાતુના બે સમાન ગોળાઓ $B$ અને $C$ પર સમાન વિદ્યુતભાર છે.જયારે આ બે ગોળાઓને એકબીજાથી અમુક અંતરે રાખવામાં આવે છે,ત્યારે તેમની વચ્ચે અપાકર્ષી બળ $F$ લાગે છે.હવે,આ ગોળાઓ જેવા જ એક ત્રીજા વિદ્યુતભાર રહિત ગોળાનો $B$ સાથે સ્પર્શ કરાવી છૂટો પાડવામાં આવે છે.ત્યારબાદ તેનો $C$ સાથે સ્પર્શ કરાવી છૂટો પાડવામાં આવે છે.ગોળા $B$ અને $C$ વચ્ચે લાગતું નવું અપાકર્ષણ બળ કેટલું હશે? (બંને ગોળા વચ્ચેનું અંતર બદલાતું નથી.)
AIEEE 2004, Diffcult
d
(d) Initially \(F = k.\frac{{{Q^2}}}{{{r^2}}}\) (fig. \(A\)). Finally when a third spherical conductor comes in contact alternately with \(B\) and \(C\) then removed, so charges on \(B\) and \(C\) are \(Q / 2\) and \(3Q / 4\) respectively (fig. \(B\))
(d) Initially \(F = k.\frac{{{Q^2}}}{{{r^2}}}\) (fig. \(A\)). Finally when a third spherical conductor comes in contact alternately with \(B\) and \(C\) then removed, so charges on \(B\) and \(C\) are \(Q / 2\) and \(3Q / 4\) respectively (fig. \(B\))
Now force \(F' = k.\frac{{\left( {\frac{Q}{2}} \right)\,\left( {\frac{{3Q}}{4}} \right)}}{{{r^2}}} = \frac{3}{8}F\)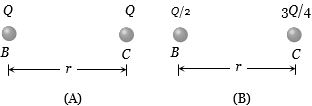
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 2જ્યારે ધાતુના તટસ્થ ગોળામાંથી $10^{14}$ ઈલેકટ્રોનસને દૂર કરવામાં આવે તો ગોળા પરનો વિદ્યુતભાર.......$\mu C$ હશે ?View Solution
- 3સમાન મૂલ્ય $0.01\,C$ ના અને $0.4\,mm$ અંતરે રાખેલા બે વિદ્યુતભારો, વિદ્યુત ડાયપોલ (દ્વિધ્રુવી) ની રચના કરે છે. જો દ્રી-ધ્રુવીને $10\,dyne/C$ ના નિયમિત વિદ્યુતક્ષેત્ર $\vec{E}$ માં, $\vec{E}$ સાથે $30^{\circ}$ ના કોણે મૂકવામાં આવે, તો દ્વિ-ધ્રુવી પર લાગતા ટોર્કનું મૂલ્ય ...... હશે.View Solution
- 4$10^{-4} \mathrm{~m}^2$ આડછેદનું ક્ષેત્રફળ ધરાવતા પાતળા ધાતુના તારનો $30 \mathrm{~cm}$ ત્રિજયાની વલય બનાવવામાં ઉપયોગ થાય છે. $2 \pi \mathrm{C}$ મૂલ્યનો ધન વીજભાર સમાન રીતે વલય પર વિતરીત થયેલ છે જ્યારે $30 \mathrm{pC}$ મૂલ્યનો ધન વીજભાર વલયના કેન્દ્ર પર રાખેલ છે. વલયમાં ઉદભવતું તણાવબળ_____$\mathrm{N}$ છે કે જેને લીધે વલયમાં વિકૃતિ ઉદ્ભવતી નથી. (ગુરૂત્વીય અસર અવગણો)$\left(\right.$ ને, $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \mathrm{SI}$ એકમ $)$View Solution
- 5View Solutionપદાર્થ ઋણ વિજભારિત ક્યારે થશે?
- 6$5\,\mu C$,$0.16\,\mu C$ અને $0.3\,\mu C$ નાં ત્રણ બિંદુવત્ત વીજભારો, કાટકોણ ત્રિકોણ કે જેની બાજુઓ $A B=3\,cm , B C=3 \sqrt{2}\,cm $ અને $C A=3\,cm$ અને $A$ એ કાટકોણ હોય તેના શિરોબિંદુ $A, B, C$ પર મૂકવામાં આવેલ છે. $A$ ઉપર રહેલો વિદ્યુતભાર બાકીના વિદ્યુતભારોને કારણે $.........N$ જેટલું સ્થિત વિદ્યુતકીય બળ અનુભવશે.View Solution
- 7જો વિર્ધુતક્ષેત્ર $10 \hat{i}+3 \hat{j}+4 \hat{k}$ આપેલ હોય તો $y z$ સમતલમાં રહેલા $10$ એકમ ક્ષેત્રફળની સપાટીમાંથી પસાર થતું વિદ્યુત ફ્લક્સ ............ એકમ હશે.View Solution
- 8જો વિંદ્યુતભાર $q$ ને અવાહક સપાટી ધરાવતા બંધ અર્ધગોળાકારનાં કેન્દ્ર આગળ મૂકવામાં આવે તો સપાટ સપાટીમાંથી પસાર થતું ફુલ ફ્લક્સ ............ થશે.View Solution
- 9એક તટસ્થ ગોળા પર $10^{12} \,\alpha$ - કણો પ્રતિ સેકન્ડ પડે છે. વિદ્યુતભાર પ્રસ્થાપિત તથા $2\ \mu C$ જેટલો વિદ્યુતભાર પ્રસ્થાપિત થવા માટે કેટલા ......$s$ નો સમય લાગશે?View Solution
- 10$0.5\, m$ ત્રિજ્યાની અર્ધ વર્તૂળ રીંગ કુલ વિદ્યુતભાર $1.4 \times 10^{-9}\, C$ થી સમાન વિદ્યુતભારીત કરેલ છે. રીંગના કેન્દ્ર આગળ વિદ્યુતક્ષેત્રની તીવ્રતા ........$V/m$ છે.View Solution
