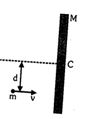
ધન $x -$ દિશા માં $(3 \,m , 0,0)$ બિંદુ પર $(0,2,0)$ બિંદુ ને અનુલક્ષીને લાગતાં $20 \,N$ મૂલ્યના બળની ચાકમાત્રા શું થાય?
Easy
c
(c)
(c)
According to the definition of torque,
\(\vec{\tau}=\vec{r} \times \vec{F}\)
Given that,the force is
\(\overrightarrow{ F }=20 \hat{i}N\)
and the arm vector is
\(\overrightarrow{ r }=(0-3) \hat{ i }+(2-0) \hat{ j }+(0-0) \hat{ k }\)
\(\overrightarrow{ r }=(-3 \hat{ i }+2 \hat{ j }) m\)
Therefore,
\(\vec{\tau}=\overrightarrow{ r } \times \overrightarrow{ F }\)
\(\vec{\tau}=\left|\begin{array}{ccc}\hat{\imath} & \hat{ j } & \hat{ k } \\-3 & 2 & 0 \\ 20 & 0 & 0\end{array}\right|=(0-0)\)
\(\hat{i}-(0-0) \hat{\hat{j}}+(0-40) \hat{ k }\)
\(|\vec{\tau}|=40 N - m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન તારમાંથી $P$ અને $Q$ રીંગ બનાવવામાં આવે છે.તેમની ત્રિજયા $r$ અને $nr$ છે. $Q$ ની જડત્વની ચાકમાત્રા $P$ કરતાં $8$ ગણી હોય,તો $n$ કેટલો હશે?View Solution
- 2જો $\mathop \omega \limits^ \to \,\, = \,\,(3\,\hat i\,\, + \,\,4\hat j\,\, + \,\,5\hat k)\,\,\,rad/s$ અને $\mathop r\limits^ \to \,\, = \,\,(\hat i - 2\hat j + 3\hat k)\,m$ હોય, તો પદાર્થના રેખીય વેગનો સદિશ .......View Solution
- 3$50\,cm$ લાંબી એક નળીમાં $250\,g$ દળ ધરાવતું અદબનીય પ્રવાહી ભરેલું છે અને તે બંને છેડાઓથી બંધ કરેલ છે. ત્યારબાદ નળીને તેના એક છેડાને ફરતે સમક્ષિતિજ સમતલમાં $x \sqrt{F} \;rad s ^{-1}$ જેટલા નિયમિત કોણીયવેગથી ભ્રમણ કરાવવામાં આવે છે. જો $F$ એ પ્રવાહી દ્વારા બીજા છેડા પર લાગતું બળ હોય તો $x$ નું મૂલ્ય થશે.View Solution
- 4એક $M$ દળની અને $R$ ત્રિન્યા વાળી વર્તુળાકાર તક્તિ સમક્ષિતિજ સમતલમાં તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ, $\omega$ કોણીય વેગથી ભ્રમણ કરે છે. જો સમાન પરિમાણ પરંતુ $\mathrm{M} / 2$ દળની બીજી તક્તિને પ્રથમ તક્તિ પબ સમાક્ષી રીતે હળવેકથી મૂકવામાં આવે તો તંત્રનો નવો કોણીય વેગ. . . . . . .છે.View Solution
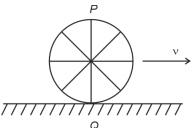
- 5નીચે દર્શાવેલ આકૃતિ મુજબ બળદગાડાનું પૈડુ એક લેવલ (સમથલ) રસ્તા ઉપર ગબડે છે. દર્શાવેલ દિશામાં જો તેની રેખીય ઝડપ $v$ હોય તો નીચેનામાંથી ક્યો વિકલ્પ સાચો છે? $(P$ અને $Q$ ક્રમશઃ પૈડાનું સૌથી ઉંચુ અને નીચુ બિંદુ દર્શાવે છે.)View Solution
- 6બે વર્તૂળાકાર રિંગના દળોનો ગુણોત્તર $1 : 2$ અને વ્યાસોનો ગુણોત્તર $ 2 : 1$ છે. તો તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર શું હોય?View Solution
- 7View Solutionકક્ષીયગતિ માં, કોણીય વેગમાન સદીશ એ ....
- 8સમાન દળ અને સમાન જાડાઈ ધરાવતી તકતીઓની ઘનતાઓ અનુક્રમે $17 \,g / cm ^3$ અને $51 \,g / cm ^3$ છે. તેમની કેન્દ્રિય અક્ષને અનુલક્ષીને તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર શું થશે?View Solution
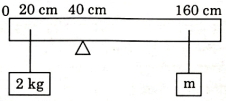
- 9$200\, cm$ લંબાઈ અને $500\, g$ દળ ધરાવતા એકસમાન સળિયાને $40\, cm$ નિશાન આગળથી ફાચર $(wedge)$ પર સંતુલિત કરવામાં આવેલ છે. $2\, kg$ ના દળને સળિયાથી $20\, cm$ અંતરે અને બીજા અજ્ઞાત દળ $m$ ને સળિયાથી $160\, cm$ નિશાની આગળથી લટકાવવામાં આવેલ છે, આકૃત્તિ જુઓ. $m$ નું એવું મૂલ્ય શોધો કે જેથી સળિયો સંતુલન સ્થિતિમાં રહે. $\left({g}=10\; m/{s}^{2}\right)$View Solution
- 10$L$ લંબાઈ અને $M$ દળની લાકડી ઘર્ષણ રહિત સપાટી પર કોઇ પણ રીતે મુક્ત પણે ગતિ કરી શકે છે. $ m$ દળનો બોલ $ v$ ઝડપથી આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે. બોલનું દળ કેટલું હોવું જોઈએ કે જેથી અથડામણ બાદ તે સ્થિર રહે ?View Solution