ધ્રુવ પ્રદેશમાં તળાવ પર બરફના સ્તરની જાડાઇ $x cm$ થી $y cm$ થતાં લાગતો સમય શોધો.વાતાવરણનું $ - {\theta ^o}C $ તાપમાન છે.
Medium
Download our app for free and get started
a
(a) Since \(t = \frac{{\rho L}}{{2k\theta }}(x_2^2 - x_1^2)\)
(a) Since \(t = \frac{{\rho L}}{{2k\theta }}(x_2^2 - x_1^2)\)
\(\therefore \)\(t = \frac{{\rho L}}{{2k\theta }}({x^2} - {y^2}) = \frac{{\rho L(x + y)(x - y)}}{{2K\theta }}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$200 \,K$ તાપમાને રહેલા પદાર્થમાંથી નીકળતા તરંગની મહત્તમ તરંગલંબાઇ $14\,\mu m$ છે, જો પદાર્થનું તાપમાન $1000 \,K$ કરતાં મહત્તમ તરંગલંબાઇ મેળવો.View Solution
- 2$l (x = 0$ થી $ x = l )$ લંબાઇના વાહકમાંથી ઉષ્મા પસાર થાય છે.તો તાપમાન વિરુધ્ધ અંતરનો આલેખView Solution
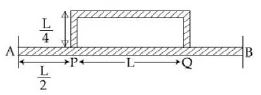
- 3$2L$ લંબાઈના એક સમાન સળીયા $AB$ ના બન્ને છેડા વચ્ચે તાપમાનનો તફાવત $120^oC$ રાખવામાં આવે છે. $AB$ સળીયા જેટલો જ આડછેદ ધરાવતો અને $\frac{3L}{2}$ લંબાઇનો એક બીજા વાંકા સળીયા $PQ$ ને આકૃતિમાં બતાવ્યા પ્રમાણે સળીયા $AB$ સાથે જોડવામાં આવે છે. સ્થાયી અવસ્થામાં $P$ અને $Q$ વચ્ચે તાપમાનનો તફાવત ....... $^oC$ ની નજીકનો હશેView Solution
- 4View Solutionતારામાંથી આવતા પ્રકાશ શું દર્શાવે છે?
- 5View Solutionમાણસના શરીર દ્વારા ઉત્સર્જન પામતા વિકિરણને ધ્યાનમાં લો. તેના માટે નીચેનામાથી શું સાચું છે?
- 6$600\,K$ તાપમાને રહેલ ગોળાને $200\,K$ તાપમાનવાળા વાતાવરણમાં મુકેલ છે.તેનો ઠંડા પડવાનો દર $H$ છે.જો તેનું તાપમાન ઘટીને $400\,K$ થાય તો તેટલા જ વાતાવરણમાં તેનો ઠંડા પડવાનો દર કેટલો થાય?View Solution
- 7એક તળાવના લંબચોરસ તળિયાની સપાટીનું ક્ષેત્રફળ $A$ છે, જેમાં પાણી (ઘનતા $=\rho,$ વિશિષ્ટ ઉષ્મા $=s$) ભરેલું છે જેની બહારની હવાનું તાપમાન $-26^{\circ} \mathrm{C}$ જેટલું અચળ છે. તળાવમાં પાણી પર બરફના સ્તરની જાડાઈ કોઈ એક સમયે $x$ છે.View Solution
બરફની ઉષ્માવાહકતા ${K}$ અને ગલનગુપ્તઉષ્મા $L$ લેવામાં આવે, તો કોઈ ક્ષણે બરફના સ્તરમાં થતાં વધારાનો દર શેના વડે આપવામાં આવે?
- 8View Solutionઉષ્મીય અવરોધનું પારિમાણિક સૂત્ર ......છે.
- 9પાત્રમાં પ્રવાહી ભરીને તેને $20°C$ તાપમાને ઓરડામાં મૂકેલ છે. જ્યારે પ્રવાહીનું તાપમાન $80°C$ હોય, ત્યારે તે $60 \,\,cal/sec$ ના દરથી ઉષ્માનો વ્યય કરે છે. જ્યારે પ્રવાહીનું તાપમાન $40°C$ હોય ત્યારે ઉષ્માના વ્યયનો દર ...... $cal/sec$ શોધો.View Solution
- 10સૂર્યને $T\; K$ તાપમાને $R$ ત્રિજ્યાનાં ગોળા તરીકે ધારતાં, સૂર્યમાંથી પૃથ્વી પર આપાત થતો કુલ ઉત્સર્જન પાવર ગણો. પૃથ્વીનું સૂર્યથી અંતર $r$ લો.View Solution
જ્યાં $r_{0}$ એ પૃથ્વીની ત્રિજ્યા અને $\sigma$ એ સ્ટીફન અચળાંક છે.