When a solid sphere having
\(\text { mass }=m\)
Radius \(=r\)
Now the Kinetic energy wllbe
The total Kinetic energy (KE) of an object is given by
\(KE =\frac{1}{2} mv ^2+\frac{1}{2} I \omega^2\)
Where I is the moment of inertia of the object and \(\omega\) is the angular momentum. For a solid sphere, the moment of inertia is given by
\(I=\frac{2}{5} m r^2\)
Angular velocity would be derived from its radius and linear velocity
\(\omega=\frac{V}{r}\)
So the total equation would
\(KE =\frac{1}{2} mv ^2+\frac{1}{2} \times \frac{2}{5} mr ^2\left(\frac{ v ^2}{ r }\right)\)
\(=\frac{1}{2} mv ^2+\frac{2}{10} mv ^2\)
To get the percentage attributed to rotational energy, we would divide the rotational part of the energy by the total energy
\(\frac{\frac{2}{10} m v^2}{\frac{1}{2} m v^2+\frac{2}{10} m v^2}=\frac{\frac{2}{10} m v^2}{\frac{7}{10} m v^2}\)
\(=\frac{2}{7}\)
Hence \(\frac{5}{7}\) is rotational and \(\frac{2}{7}\) translational.
Download our appand get started for free
Similar Questions
- 1$5\,kg$નું એક બાળક ચકડોળમાં ફરે છે જે $3.14\,s$ માં $1$ પરિભ્રમણ પૂર્ણ કરે છે. ચકડોળની ત્રિજ્યા $2\,m$ છે. બાળક પર લાગતું કેન્દ્રત્યાગી બળ $.......\,N$ હશેView Solution
- 2એક એન્જિનની મોટર પોતાની ધરીને અનુલક્ષીને $100\ rpm$ ની કોણીય ઝડપે ફરે છે. તેની સ્વિચ બંધ કરતાં $15\ s$ માં સ્થિર થાય છે, તો તે ....... પરિભ્રમણો બાદ સ્થિર થઈ હશે .View Solution
- 3$1\ kg $ અને $3\ kg$ આંતરિક બળોના કારણે એકબીજા તરફ ગતિ કરે છે.જયારે તેમનો સાપેક્ષ વેગ $2\ m/s$ હોય,ત્યારે દ્રવ્યમાન કેન્દ્ર નો વેગ $0.5\ m/s$ છે.તો જયારે તેમનો સાપેક્ષ વેગ $3\ m/s$ હોય,ત્યારે દ્રવ્યમાન કેન્દ્ર નો વેગ ......... $m/s$ થાય.View Solution
- 4$m_1$ અને $m_2$ $(m_1 > m_2)$ દળના બે કણો સ્થિર સ્થિતિમાથી શરૂ કરીને એકબીજા તરફ આકર્ષીબળ ના વ્યસ્ત વર્ગના નિયમ મુજબ ગતિ કરે છે. આ તંત્ર માટે દ્રવ્યમાન $(CM)$ કેન્દ્ર માટે નીચેનામાથી સાચું વિધાન પસંદ કરો.View Solution
- 5જો પૃથ્વીનું દળ અચળ રાખી ત્રિજ્યા અડધી કરવામાં આવે તો દિવસનો સમયગાળો ........ $hr$ થશે.View Solution
- 6એક સમક્ષિતિજ તક્તી (ડિસ્ક) તેના કેન્દ્ર માંથી પસાર થતી ઊર્ધ્વ અક્ષને અનુલક્ષીને પ્રતિ મિનિટે $90$ પરિભ્રમણોના દરે મુક્તપણે ભ્રમણ કરે છે. એેક $m$ દળના મીણ નો નાનો ટુકડો તકતી પર શિરોલંબ રીતે પડે છે અને તે અક્ષ થી $r$ અંતરે ચોંટે છે. જો પ્રતિ મિનિટે પરિભ્રમણો ની સંખ્યા $60$ સુધી ઘટે તો તકતી ના જડત્વની ચાકમાત્રા શું થાય?View Solution
- 7એક વર્તુળાકાર તક્તિ સમક્ષિતિજ સમતલ પર કોણીય વેગ $\omega$ સાથે એવી રીતે ગતિ કરે છે, કે જેની અક્ષ તેના કેન્દ્રમાંથી પસાર થાય અને તક્તિને લંબ હોય. એક વ્યક્તિ તેના કેન્દ્ર પર બેસીને હાથ વડે બે ડંબેલોને ધરાવે છે. જયારે તે તેના હાથને ખેંચે છે ત્યારે તેની જડત્વની ચાકમાત્રા ત્રણ ગણી થાય છે. જો $E$ તંત્રની શરૂઆતની ગતિ ઊર્જા હોય, તો અંતિમ ગતિ ઊર્જા $\frac{E}{x}$ હશે. જ્યાં $x$ નું મૂલ્ય ........ છે.View Solution
- 8View Solutionએક પાતળી વર્તુળાકાર વીટી સૌપ્રથમ એક ઢોળાવયુક્ત સપાટી ઉપરથી નીચે સરકે છે અને ત્યાર બાદ તેજ ઊંચાઈથી સમાન ભૂમિતિના એક ખરબચડા ઢોળાવ ઉપરથી નીચે ગબડે છે. બે ગતિઓમાં લેવાયેલ સમયનો ગુણોત્તર શું થાય?
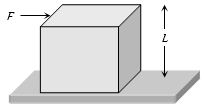
- 9$L$ લંબાઇનો સમઘન બ્લોક $\mu $ ઘર્ષણાક ધરાવતી સપાટી પર પડેલો છે આકૃતિમાં દર્શાવ્યા મુજબ એક બળ $F$ લગાવવામાં આવે છે. જો ઘર્ષણાક નું મૂલ્ય એટલું ઊંચું હોય કે જેથી બ્લોક ખ્સયા પહેલા ઢળી પડે તો તેના માટે ન્યૂનતમ $F$ નું મૂલ્ય કેટલું હોવું જોઈએ ?View Solution
- 10પ્રત્યેકનું દળ $1 \mathrm{~kg}$ હોય તેવા ચાર કણોને $2 \mathrm{~m}$ બાજુ ધરાવતા ચોરસના ચાર ખૂણા પર મૂકેલા છે. તેના એક શિરોબિંદુમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને તંત્રની જડત્વની ચાક્માત્રા______$\mathrm{kg} \mathrm{m}^2$છે.View Solution