એક પાતળી વર્તુળાકાર વીટી સૌપ્રથમ એક ઢોળાવયુક્ત સપાટી ઉપરથી નીચે સરકે છે અને ત્યાર બાદ તેજ ઊંચાઈથી સમાન ભૂમિતિના એક ખરબચડા ઢોળાવ ઉપરથી નીચે ગબડે છે. બે ગતિઓમાં લેવાયેલ સમયનો ગુણોત્તર શું થાય?
Medium
c
(c)
(c)
case \((i)\) Transitional motion
acceleration \(=g \sin \theta\)
case \((ii)\) acceleration \(=\frac{ g \sin \theta}{1+\frac{1}{ MR ^2}}\)
\(I = MR ^2\)
\(a =\frac{ g \sin \theta}{2}\)
Now using \(\rho=u t+\frac{1}{2} at ^2\)
\(a _1 t _1^2= a _2 t _2^2 \quad \theta\) and \(\rho\) same for both are and \(v =0\)
\(\frac{ t _1{ }^2}{ t _2^2}=\frac{ a _2}{ a _1}=\frac{ g \sin \theta}{2 g \sin \theta}\)
\(\frac{t_1}{t_2}=\frac{1}{\sqrt{2}}\)
\(\therefore \frac{t_1}{t_2}=\frac{1}{\sqrt{2}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉદગમબિંદુ થી $(3\hat i + 2\hat j - 4\hat k)$ $m$ અંતરે $(2\hat i - 4\hat j + 2\hat k)$ $N$ બળ લાગે તો ટોર્ક નું મૂલ્ય ....... $ N-m$ થાય.View Solution
- 2$3 \;kg$ દળ અને $40\; cm$ ત્રિજયાના એક પોલા નળાકારની ફરતે દોરી વીંટાળેલ છે. જો આ દોરીને $30\;N$ બળ આપીને ખેંચવામાં આવે, તો નળાકારનો કોણીય પ્રવેગ ($rad/sec^2$ માં) કેટલો થાય?View Solution
- 3એક મોટરસાઇકલ રોડ પર $ 54\;kmh^{-1}$ ની ઝડપથી ગતિ કરે છે. તેના પૈડાઓની ત્રિજયા $0.45\;m$ અને તેના ભ્રમણ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $3 \;kgm^2$ છે. જો આ વાહન $15$ સેકન્ડમાં સ્થિર થાય, તો બ્રેક દ્વારા પૈડા પર લાગતા સરેરાશ ટોર્કનું મૂલ્ય ($kg\,m^2\,s^{-2}$ માં) કેટલું હશે?View Solution
- 4View Solutionઢાળ પરથી સરક્યાં વગર ગબડતા નળાકારના કોણીય વેગમાન માટે નીચેનામાથી શું સાચું છે?
- 5સમક્ષિતિ સપાટી પર ગબડતી $50 \mathrm{~kg}$ દળની એક તકતીના દ્રવ્યમાનકેન્દ્રનો વેગ $0.4 m/s$ છે તો આ તકતી ને અટકાવવા માટે કરવું પડતું કાર્ય ........... $J$View Solution
- 6View Solutionએક નળાકર બે સમાન ઊંચાઈ ધરાવતા પરતું જુદાં જુદાં ખૂણાઓ ધરાવતાં ઢોળાવવાળા સમતલ ઉપરથી નીચે ગબડે છે.
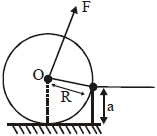
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણે $M$ દળ અને $R$ ત્રિજ્યા ધરાવતો એકસમાન નળાકારને $a$ ($a < R$) ઊંચાઈ પર $F$ જેટલું બળ at its centre $'O'$View Solution
- 8અવગણ્ય દ્રવ્યમાન ધરાવતા $1 \;m$ લંબાઈના એક જડ સળિયાના બે છેડા પર અનુક્રમે $5\, kg$ અને $10\, kg$ દ્રવ્યમાનના કણો જોડેલ છે. $5\, kg$ ના કણથી આ તંત્રનું દ્રવ્યમાન કેન્દ્ર આશરે કેટલા અંતરે ($m$ માં) હશે?View Solution
- 9$L$ લંબાઇનો સળિયા બે માણસના ખંભા પર છે. છેડા પરના એક માણસ પર $ 1\over 4 $ માં ભાગનું વજનબળ લાગે છે. તો બીજો માણસ આ છેડાથી કેટલે દૂર હશે?View Solution
- 10View Solutionનૃત્યકાર ચાકગતિ કરતા પ્લેટફોર્મ પર હાથમાં બે ગોળા લઈને ઊભો છે. જો તે ગોળા જમીન પર પડી જાય તો નૃત્યકારની...
