દરેકની સમાન કેન્દ્રલંબાઇ $f$ વાળા કાચ $\left( {{\mu _g} = \frac{3}{2}} \right)$ ના સમ બર્હિગોળ લેન્સ એકબીજાના સંપર્કમાં મૂકેલાં છે. બંને લેન્સો વચ્ચેની જગ્યામાં પાણી (${\mu _w} = \frac{4}{3}$) ભરેલું છે. આ સંયોજનની કેન્દ્રલંબાઇ કેટલી હશે?
NEET 2016, Diffcult
b
\(\text { Here, } \mu_{g}=\frac{3}{2}, \mu_{w}=\frac{4}{3}\)
\(\text { Here, } \mu_{g}=\frac{3}{2}, \mu_{w}=\frac{4}{3}\)
Focal length \((f)\) of glass convex lens is given by
\(\frac{1}{f}=\left(\mu_{g}-1\right)\left(\frac{2}{R}\right)\)
or \(\frac{1}{f}=\left(\frac{3}{2}-1\right) \frac{2}{R}=\frac{1}{R}\) or \(f=R.........(i)\)
Focal length \((f)\) of water filled concave lens is given by
\(\frac{1}{f^{\prime}} =\left(\mu_{w}-1\right)\left(-\frac{2}{R}\right) \text { or } \frac{1}{f^{\prime}}=\left(\frac{4}{3}-1\right)\left(-\frac{2}{R}\right) \)
\(=-\frac{2}{3 R}=-\frac{2}{3 f} \quad[\text { Using } \operatorname{eqn} .(\mathrm{i})]\)
Equivalent focal length \(\left(f_{e q}\right)\) of lens system \(\frac{1}{f_{e q}}=\frac{1}{f}-\frac{2}{3 f}+\frac{1}{f}=\frac{3-2+3}{3 f}=\frac{4}{3 f}\)
\(\therefore f_{e q}=\frac{3 f}{4}\)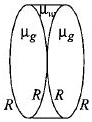
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$-15 \,D$ અને $5\, D$ પાવરના બે લેન્સને એકબીજાના સંપર્કમાં રાખેલા છે. આ જોડાણની કેન્દ્રલંબાઈ .......$cm$ થશે.View Solution
- 2$100\, cm$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સ અને $10\, cm$ કેન્દ્રલંબાઈના અંતર્ગોળ લેન્સને સમાન સક્ષ પર $90 \,cm$ અંતરે દુર મૂકવામાં આવ્યા છે. જો પ્રકાશના સમાંતર કિરણપૂંજને બહિર્ગોળ લેન્સ પર આપાત કરવામા આવે, તો બે લેન્સમાંથી પસાર થયા બાદ કિરણ પૂંજView Solution
- 3$f$ કેન્દ્રલંબાઈનો અંતર્ગોળ લેન્સ વસ્તુના કદ થી $(1/x)$ ગણુ પ્રતિબિંબ રચે છે. લેન્સથી વસ્તુનું અંતર કેટલું છે ?View Solution
- 4View Solutionનીચેનામાંથી ક્યુ વિધાન સાચુ છે ?
- 5$f$ કેન્દ્રલંબાઈનો અંતર્ગોળ અરીસો વસ્તુના કદ કરતા $n$ ગણું પ્રતિબિંબ રચે છે. જો પ્રતિબિંબ વાસ્તવિક હોય, તો અરીસાથી વસ્તુનું અંતર કેટલું છે ?View Solution
- 6ટેલિસ્કોપના વસ્તુકાંચની કેન્દ્રલંબાઈ $150\,\,cm$ અને નેત્રકાંચની કેન્દ્રલંબાઈ $5 \,\,cm$ છે. જો $1\,\,km$ અંતરે રહેલ $50\,\,m$ ઊંચી વસ્તુને આ ટેલિસ્કોપ વડે જોવામાં આવે ત્યારે ટાવરના પ્રતિબિંબ વડે બનતો ખૂણો $\theta $, હોય તો $\theta $ નું મૂલ્ય $^o$ માં લગભગ કેટલું હશે?View Solution
- 7ટેલિસ્કોપમાં ઓબ્જેક્ટિવ લેન્સની અને આઇપીસની કેન્દ્રલંબાઈ $15\;cm$ અને $10\;mm$ છે,જો ટ્યુબલંબાઈ $16\;cm$ હોય તો ટેલિસ્કોપની મોટવણી કેટલી થશે?View Solution
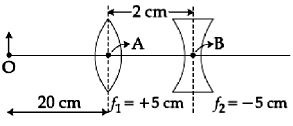
- 8આકૃતિમાં દર્શાવેલ લેન્સના સંયોજનથી કયા સ્થાન પર અને કેવું પ્રતિબિંબ રચાશે? ($f_1, f_2$ એ કેન્દ્ર લંબાઈ છે.)View Solution
- 9$15\, cm $ કેન્દ્રલંબાઈના બહિર્ગોળ અરીસા અને $10\, cm$ લંબાઈના અંત:ર્ગોળ અરીસાને એકબીજાથી સામ સામે $40\, cm$ અંતરે મૂકેલા છે. એક બિંદુવત્ વસ્તુને અરીસાઓની વચ્ચે તેઓની સામાન્ય અક્ષ પર અને અંત:ર્ગોળ અરીસાથી $15\, cm$ ના અંતરે મૂકવામાં આવે છે. પરાવર્તન દ્વારા ઉત્પન્ન થતાં પ્રતિબિંબનું સ્થાન બહિર્ગોળ અરીસા પાસે .....$cm$ અંતરે હશે.View Solution
- 10$100\,W$ તથા $5\,\%$ પાવર ધરાવતા બલ્બ એ જોઈ શકાય તેવું વિકીરણ પેદા કરે છે.તો $10\,m$ ના અંતરે સરેરાશ જોઈ શકાય તેવા વિકીરણની તીવ્રતાView Solution
