ટેલિસ્કોપના વસ્તુકાંચની કેન્દ્રલંબાઈ $150\,\,cm$ અને નેત્રકાંચની કેન્દ્રલંબાઈ $5 \,\,cm$ છે. જો $1\,\,km$ અંતરે રહેલ $50\,\,m$ ઊંચી વસ્તુને આ ટેલિસ્કોપ વડે જોવામાં આવે ત્યારે ટાવરના પ્રતિબિંબ વડે બનતો ખૂણો $\theta $, હોય તો $\theta $ નું મૂલ્ય $^o$ માં લગભગ કેટલું હશે?
JEE MAIN 2015, Diffcult
c
Magnifying power of telescope,
Magnifying power of telescope,
\(M P=\frac{\tan \beta( \text { angle subtended by image at eye piece) } }{\tan \alpha \text { (angle subtended by object on objective) }}\)
Also, \(M P =\frac{f_{o}}{f_{e}}=\frac{150}{5}=30\)
\(\tan \alpha =\frac{50}{1000}=\frac{1}{20}\, \mathrm{rad}\)
\(\therefore \quad \tan \beta=\theta=M P \times \tan \alpha\)
\(=30 \times \frac{1}{20}=\frac{3}{2}=1.5\)
or, closest value of \(\beta \approx 60^o\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$100\, cm$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સ અને $10\, cm$ કેન્દ્રલંબાઈના અંતર્ગોળ લેન્સને સમાન સક્ષ પર $90 \,cm$ અંતરે દુર મૂકવામાં આવ્યા છે. જો પ્રકાશના સમાંતર કિરણપૂંજને બહિર્ગોળ લેન્સ પર આપાત કરવામા આવે, તો બે લેન્સમાંથી પસાર થયા બાદ કિરણ પૂંજView Solution
- 2એક વિદ્યાર્થી બર્હિગોળ લેન્સની સામે $‘u’$ જેટલા અંતરે એક પિન મુખ્ય અક્ષને લંબ મૂકીને જુદાં જુદાં વસ્તુઅંતરો માટે અનુરૂપ પ્રતિબિંબઅંતરો $‘v’$ માપે છે.આ વિદ્યાર્થી દ્રારા દોરવામાં આવેલ $v$ વિરુદ્ઘ $u$ નો આલેખ કયો હશે?View Solution
- 3$3mm$ જાડાઇ અને $6cm$ વ્યાસ ધરાવતા સમતલ બર્હિગોળ લેન્સમાં પ્રકાશની ઝડપ $ 2\times 10^8 m/sec$ હોય,તો તેની કેન્દ્રલંબાઇ કેટલા ......$cm$ હશે.View Solution
- 4View Solutionકોંચી વિભેદન (The Cauchy’s dispersion) સૂત્ર કયુ છે.
- 5$1.5$વકીભવનાંકવાળા દ્વિ-બહિર્ગોળ લેન્સની હવામાં કેન્દ્ર લંબાઈ $20 \mathrm{~cm}$ છે. જ્યારે તેને$1.6$ વક્રીભવનાંક ધરાવતા પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે તેની કેન્દ્ર લંબાઈ__________થશે.View Solution
- 6View Solutionજો અજ્ઞાત દ્રવ્ય અને અજ્ઞાત કેન્દ્રલંબાઈ ધરાવતા સમતલ બહિર્ગોળ લેન્સ આપેલ હોય તો સ્ફેરોમીટરથી શું માપી શકાય?
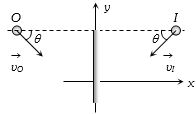
- 7જો એક વસ્તુ સમતલ અરીસાની તરફ $v$ વેગથી અરીસાની લંબ દિશા સાથે $\theta $ ખૂણે ગતિ કરે, તો તે વસ્તુ અને પ્રતિબિંબ વચ્ચેનો સાપેક્ષ વેગ કેટલો થાય?View Solution
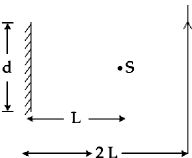
- 8એક દિવાલ પર શિરોલંબ લટકાવેલ $d$ પહોળાઇના એક સપાટ અરિસાના કેન્દ્રની સામે $L$ અંતર પર પ્રકાશનો એક બિંદુવત ઉદગમ $S$ મુકેલ છે. આ અરિસાથી $2L$ અંતરે એક સમાંતર રેખા પર અરિસાની સામેથી એક માણસ પસાર થાય છે આ માણસને અરિસામાં પ્રકાશના ઉદગમનું પ્રતિબિંબ ક્યા અંતરે દેખાશે ?View Solution
- 9એક સમાંતર પ્રકશકિરણને $30 \,cm$ જેટલો વ્યાસ અને $1.5$ જેટલો વક્રીભવનાંક ધરાવતા પારદર્શક ગોલીય ગોળા ઉપર પડવા દેવામાં આવે છે. ગોળાના કેન્દ્રથી ............ $mm$ અંતરે પ્રકાશ કિરણપૂંજ કેન્દ્રિત થશે.View Solution
- 10બર્હીગોળ લેન્સની વક્રતાની ત્રિજ્યાનું મૂલ્ય $20\,cm$ છે. તેની સામે $2\,cm$ ની ઉંચાઈએ લેન્સથી $30\,cm$ વસ્તુ મુકતા મળતા પ્રતિબિંબને નીચેનામાંથી કયો વિકલ્પ શ્રેષ્ઠ રીતે દર્શાવે?View Solution
