દ્રવ્યના પોઈસનનો ગુણોત્તર $0.5$ છે. સળીયો લંબાઈને અનુલક્ષીને $3 \times 10^{-3}$ જેટલો વિકૃતિ અનુભવે છે તો તેના કદમાં થતો વધારો ............... $\%$ હશે.
Medium
d
(d)
(d)
\(\frac{\text { Lateral strain }}{\text { Longitudinal strain }}=\eta=0.5\)
\(\frac{-\Delta r / r}{\Delta l / l}=\frac{1}{2}\)
\(\frac{-2 \Delta r}{r}=\frac{\Delta l}{l}\)
Magnitute wise both are equal but sign's would be different as both quantities cannot increase
Now volume \(\propto\) area \(\times\) length \(v \propto r^2 \cdot L\)
\(\frac{\Delta V}{V}=\frac{2 \Delta r}{r}+\frac{\Delta L}{L}\)
Substituting value of \(\frac{\Delta L}{L}\)
\(\frac{\Delta V}{V}=0\)
\(\therefore\) No change in volume.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1તાર $A$ અને $B$ નાં દ્રવ્યના યંગ ગુણાંકોનો ગુણોત્તર $1:4$ છે, જ્યારે તેમના આડછેદના ક્ષેત્રફળનો ગુણોત્તર $1:3$ છે. જો બંને તારને સમાન મૂલ્યના બોજ લગાડવામાં આવે, તો તાર $A$ અને $B$ માં ......... ગુણોત્તરમાં ખેંચાણ (લંબાઈ વધારો) ઉદભવશે. [તાર $A$ અને $B$ સમાન લંબાઈ ધારો.]View Solution
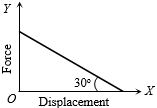
- 2View Solutionતાર માટે બળ વિરુધ્ધ સ્થાનાંતરનો આલેખ આપેલ છે,તો તારનો બળ અચળાંક કેટલો થાય?
- 3બે સમાન દ્રવ્યમાથી બનાવેલા તાર જેના વ્યાસનો ગુણોત્તર $n:1$ છે બંને તારની લંબાઈ $4\,m$ છે બંને પર સમાન બળ લગાવવામાં આવે તો પાતળા તારની લંબાઈમાં થતો વધારો કેટલો હોય $?$View Solution
- 4View Solutionસંપૂર્ણ કઠોર પદાર્થ માટે યંગ મોડયુલસનું મૂલ્ય ............... છે.
- 5View Solutionકયો સ્થિતિસ્થાપકતા અંક પ્રવાહી માટે વપરાય છે.
- 6View Solutionહુકના નિયમ અનુસાર બળ કોના સમપ્રમાણ માં હોય ?
- 7બે અલગ દ્રવ્યમાથી બનેલા સળિયાનો રેખીય પ્રસરણ અચળાંક ${\alpha _1},\,$ અને ${\alpha _2}$ અને યંગ મોડ્યુલસ ${Y_1}$ અને ${Y_2}$ છે સળિયાને બે દઢ દીવાલ સાથે જડિત કરેલો છે .બંનેને એવી રીતે ગરમ કરવામાં આવે છે કે જેથી બંનેના તાપમાનમા સમાન રીતે વધારો થાય અને તારમાં વંકન થતું નથી. જો ${\alpha _1}:{\alpha _2} = 2:3$, અને બંને માં સમાન સમાન તાપીય પ્રતિબળ ઉત્પન્ન થતું હોય તો ${Y_1}:{Y_2}$ $=$_____View Solution
- 8View Solutionજો પદાર્થ માટે યંગ મોડ્યુલસ શૂન્ય હોય તો પદાર્થ કઈ અવસ્થામાં હોય ?
- 9દ્રવ્યની સામાન્ય ઘનતા $\rho$ અને સ્થિતિસ્થાપકતાનો આયતન માપાંક (bulk modulus of elasticity) $K$ છે. જ્યારે બધીજ બાજુંએથી પદાર્થ પર એક સમાન દબાણ $P$ લાગૂ પાડવામાં આવે ત્યારે દ્રવ્યની ઘનતામાં થતાં વધારાનું મૂલ્ય કેટલું હશે?View Solution
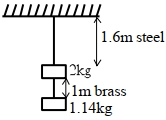
- 10પ્રત્યેકની ત્રિજ્યા $0.2\,cm$ અને દળ અવગણ્ય હોય તેવા સ્ટીલ અને પિત્તળમાંથી બનાવેલા બે તારને આકૃત્તિમાં દર્શાવ્યા મુજબ ભારિત કરેલા છે. સ્ટીલના તારનું ખેંચાણ $......\times 10^{-6}\,m$ છે.(સ્ટીલનો યંગ ગુણાંક $=2 \times 10^{11}\,Nm ^{-2}, g=10\,ms ^{-2}$)View Solution