એઝો આઈસોપ્રોપેન નીચેનાં સમીકરણ મુજબ વિઘટન પામે છે .
${(C{H_3})_2}CHN\,\, = \,\,NCH{(C{H_3})_2}(g)\,\xrightarrow{{250\,\, - \,\,{{290}\,^o }C}}\,{N_2}(g)\,\, + \,\,{C_6}{H_{14}}(g)$
તે પ્રથમ ક્રમની પ્રક્રિયા છે. જો પ્રારંભિક દબાણ $P_o $ અને $t $ સમયે મિશ્રણનું દબાણ $(P_t) $ છે. તો દર અચળાંક $K $ શોધો.
Diffcult
Download our app for free and get started
a
$\begin{array}{*{20}{c}}
{{{(C{H_3})}_2}CHN{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} NCH{{(C{H_3})}_2}(g){\mkern 1mu} } \\
\begin{gathered}
\,\,\,{p_o} \hfill \\
{p_{o - x}} \hfill \\
\end{gathered}
\end{array}$ $\xrightarrow{{250{\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} 290{{\kern 1pt} ^o}C}}{\mkern 1mu} $ $\begin{array}{*{20}{c}}
{{N_2}(g) + {\mkern 1mu} {\mkern 1mu} {C_6}{H_{14}}(g)} \\
\begin{gathered}
0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \hfill \\
x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \hfill \\
\end{gathered}
\end{array}{\mkern 1mu} {\mkern 1mu} $
$\begin{array}{*{20}{c}}
{{{(C{H_3})}_2}CHN{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} NCH{{(C{H_3})}_2}(g){\mkern 1mu} } \\
\begin{gathered}
\,\,\,{p_o} \hfill \\
{p_{o - x}} \hfill \\
\end{gathered}
\end{array}$ $\xrightarrow{{250{\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} 290{{\kern 1pt} ^o}C}}{\mkern 1mu} $ $\begin{array}{*{20}{c}}
{{N_2}(g) + {\mkern 1mu} {\mkern 1mu} {C_6}{H_{14}}(g)} \\
\begin{gathered}
0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \hfill \\
x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \hfill \\
\end{gathered}
\end{array}{\mkern 1mu} {\mkern 1mu} $
${p_0 - x+x+x=P_t}$
${x=P_t-P_0}$
$K\,\, = \,\,\frac{{2.303}}{t}\log \frac{{{P_0}}}{{{P_0}\, - \,\,x}}\,\, = \,\,\frac{{2.303}}{t}\log \frac{{{P_0}}}{{2{P_0}\, - \,\,{P_t}}}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રથમ ક્રમની પ્રક્રિયા માટે,$90\%$ પ્રક્રિયા પૂર્ણ થવા માટે લાગતો સમય, પ્રક્રિયાના અર્ધ આયુષ્ય કરતા ' $x$ ' ગણો છે. તો ' $x$ નું મૂલ્ય શોધો. (આપેલ: $\ln 10=2.303$ અને $\log 2=0.3010$ )View Solution
- 2$25\,^oC$ એ દર અચળાંક, સક્રિયકરણ ઊર્જા અને રાસાયણિક પ્રક્રિયાનાં આર્હેંનિયસ પરિબળો અનુક્રમે $3.0\times 10^{-4} \,s^{-1}, 104.4 \,kJ$ મોલ$^{-1} $ અને $6.0 \times 10^{14}\, s^{-1}$ છે. તો $T\rightarrow \infty$ તરીકે દર અચળાંકનું મૂલ્ય શોધો.View Solution
- 3તાપમાનમાં પ્રતિ $10\,^o C$ નો વધારો કરતા એક પ્રક્રિયાનો વેગ બે ગણો થાય છે. જો તાપમાનમાં $50\,^o C$ નો વધારો કરવામાં આવે, તો પ્રક્યિાનો વેગ લગભગ .......... ગણો વધશે.View Solution
- 4નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.View Solution
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
સ્ટેપ Rate constant $\left(\sec ^{-1}\right)$
Activation energy
$\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
$1$ ${k}_1$ $300$ $2$ ${k}_2$ $200$ $3$ ${k}_3$ $\mathrm{Ea}_3$ ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).
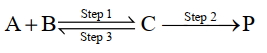
- 5પ્રથમ ક્રમની એક પ્રકિયા $15\,\min$ માં $75\%$ પૂર્ણ થાય, તો પ્રક્રિયાને $90\%$ પૂર્ણ થતા ........... $\min$ લાગશે.View Solution
- 6પ્રક્રિયા $2NO + O_2 \rightarrow NO_2$ એ કઇ પ્રક્રિયાનો ઉદાહરણ છે. ?View Solution
- 7પ્રથમ ક્રમની એક પ્રક્રિયા પ્રક્રિયકના ડેસીમોલર દ્રાવણથી શરૂ થાય છે. $8$ મિનિટ બાદ તેની સાંદ્રતા $M/100$ થાય, તો પ્રક્રિયાનો વેગ અચળાંક જણાવો.View Solution
- 8View Solutionબેઝિક માધ્યમમાં એસ્ટરનુ જળવિભાજન ........ પ્રક્રિયા છે.
- 9પ્રથમ ક્રમ પ્રક્રિયાનો આર્હેનિયસ આલેખ $\left(\ln \mathrm{k}\,\, \mathrm{v} / \mathrm{s} \,\,\frac{1}{\mathrm{~T}}\right)$નો ઢાળ $-5 \times 10^{3} \,\mathrm{~K}$ છે. પ્રક્રિયાના $\mathrm{E}_{\mathrm{a}}$ નું મૂલ્ય શું છે ? તમારા જવાબ માટે સાચો વિકલ્પ પસંદ કરો.($\mathrm{~kJ} \mathrm{~mol}^{-1}$ માં)View Solution
$\left[\right.$ આપેલ $\left.\mathrm{R}=8.314 \,\mathrm{JK}^{-1} \,\mathrm{~mol}^{-1}\right]$
- 10પ્રથમક્રમની પ્રક્રિયા માટે શરૂઆતની સાંદ્રતામાં $1/4$ જેટલો ઘટાડો થવા માટે લાગતો સમય $20$ મિનિટ છે. તો શરૂઆતની સાંદ્રતા માં $1/16 $ જેટલો ઘટાડો થવા માટે લાગતો સમય......... $\min.$ હશે.View Solution