નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
| સ્ટેપ |
Rate constant $\left(\sec ^{-1}\right)$ |
Activation energy $\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$ |
| $1$ | ${k}_1$ | $300$ |
| $2$ | ${k}_2$ | $200$ |
| $3$ | ${k}_3$ | $\mathrm{Ea}_3$ |
ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).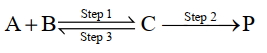
JEE MAIN 2024, Medium
Download our app for free and get started
c
\(\mathrm{K}=\frac{\mathrm{K}_1 \mathrm{~K}_2}{\mathrm{~K}_3}\)
\(\mathrm{K}=\frac{\mathrm{K}_1 \mathrm{~K}_2}{\mathrm{~K}_3}\)
\(A \mathrm{e}^{\frac{-\mathrm{E}_2}{\mathrm{RT}}}=\frac{\mathrm{A}_1 \mathrm{e}^{\frac{-\mathrm{E}_{\mathrm{a}_1}}{\mathrm{RT}}} \mathrm{A}_2 \mathrm{e}^{\frac{-\mathrm{E}_{2_2}}{\mathrm{RT}}}}{\mathrm{A}_3 \mathrm{e}^{\frac{-\mathrm{E}_{\mathrm{a}_1}}{\mathrm{RT}}}}\)
\(A \mathrm{e}^{\frac{-\mathrm{E}_2}{\mathrm{RT}}}=\frac{\mathrm{A}_1 \mathrm{~A}_2}{\mathrm{~A}_3} \mathrm{e}^{\frac{-\left(\mathrm{E}_{\mathrm{a}_2}+\mathrm{E}_{\mathrm{a}_2}-\mathrm{E}_{\mathrm{E}_3}\right)}{\mathrm{RT}}}\)
\(\mathrm{E}_{\mathrm{a}}=\mathrm{E}_{\mathrm{a}_1}+\mathrm{E}_{\mathrm{a}_2}-\mathrm{E}_{\mathrm{a}_3}\)
\(400=300+200-\mathrm{E}_{\mathrm{a}_3}\)
\(\mathrm{E}_{\mathrm{a}_3}=100 \mathrm{~kJ} / \mathrm{mole}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સાદી રાસાયણિક પ્રક્રિયા $A \rightarrow B$ માટે પુરોગામી પ્રક્રિયાની સક્રિયકરણ ઊર્જા $E_a$ છે. તો પ્રતિગામી પ્રક્રિયાની સક્રિયકરણ ઊર્જા ............View Solution
- 2View Solutionજુદા-જુદા પ્રક્રિયકો ધરાવતી પ્રક્રિયા કદાપી...... ન હોઈ શકે ?
- 3પ્રથમ કમની પ્રક્રિયાનો વેગ અવળાંક $6\,\min^{-1}$ છે. જો પ્રકિયકની શરૂઆતની સાંદ્રતા $0.5\, mol\, L^{-1}$ છે. તો ...... $\min$ પછી પ્રક્રિયકની સાંદ્રતા $0.05\, mol\,L^{-1}$ થશે ?View Solution
- 4રાસાયણિક પ્રક્રિયા $A \rightarrow B$ માટે પુરોગામી દિશામાં સક્રિયકરણ ઉર્જા $Ea$ છે. તો પ્રતિગ્રામી દિશામાં સક્રિયકરણ ઉર્જા.........View Solution
- 5શૂન્ય ક્રમતી એક પ્રક્રિયાતો વેગ અચળાંક $2.0\times10^{-2}\, mol\, L^{-1}\, s^{-1}$ છે. જો $25\, seconds$ પછી પ્રક્રિયાની સાંદ્રતા $0.5\, M$ હોય તો શરૂઆતની સાંદ્રતા ......... $M$ માં શું હશે ?View Solution
- 6ઓછા દબાણ પર ટંગસ્ટન પર ફોસ્ફિન $(PH_3)$ ના વિઘટન એ પ્રથમ ક્રમની પ્રક્રિયા છે.કારણ કે.....View Solution
- 7View Solutionપ્રથમક્રમ પ્રક્રિયાનો વિશિષ્ટ દર અચળાંક ....... પર આધારિત છે.
- 8પક્રિયા $2 NO + Br _2 \rightarrow 2 NOBr$View Solution
નીચે આપેલ પ્રક્કિયાવિધી દ્વારા થઈ રહી છે.
$NO + Br _2 \Leftrightarrow NOBr _2 \text { (fast) }$
$NOBr _2+ NO \rightarrow 2 NOBr$(ધીમી)
પ્રક્રિયાનો સમગ્ર ક્રમ $........$
- 9જો $75\%$ પ્રથમ ક્રમ પ્રક્રિયા $32$ મિનિટમાં પુરી થાય તો એ જ પ્રક્રિયા $50\%$ પુરી થવા કેટલી મિનિટ લાગશે.View Solution
- 10નીચે આપેલ વિધાન/નો ની સંખ્યા કે જે સાચા છે તે $......$View Solution
$A$.વેગ અચળાંક નો તાપમાન પર આધાર પ્રબળ, સક્રિયકરણ શક્તિ (ઊર્જા) ઊચી હોય છે
$B$.જો પ્રક્રિયા શૂન્ય સક્રિકરણ શક્તિ ધરાવે, તો તેનો વેગ તાપમાન થી સ્વતંત્ર છે
$C$.વેગ અચળાંક નો તાપમાન પર આધાર પ્રબળ, સક્રિયકરણ શક્તિ (ઊર્જા) નીચી હોય છે
$D$.જો તાપમાન અને વેગ અયળાંક વચ્ય જો સહસંબંધ ના હોય તો પછી તેનો ઈ અર્થ થાય છે કે પ્રક્રિયા ઋણ સક્રિયકરણ શક્તિ ધરાવે છે.