એક બંધ પરિપથમાં $t$ સમયે વિધુતપ્રવાહ $I = 4 - 0.08\ t$ છે, તો વાહકના આડછેદમાંથી $50$ સેકન્ડમાં પસાર થતા ઇલેક્ટ્રોનની સંખ્યા......થશે.
Medium
Download our app for free and get started
b
\(I\,\, = \,\,\frac{{dQ}}{{dt}}\,\, = \,\,4\,\, - \,\,0.08t\)
\(I\,\, = \,\,\frac{{dQ}}{{dt}}\,\, = \,\,4\,\, - \,\,0.08t\)
\(\therefore \,\,dQ\, = \,\,(4\,\, - \,\,0.08t)\,dt\,\)
\(\,\therefore \,\,Q\,\, = \,\,\int\limits_0^{50} {(4\, - \,0.08t)} \,dt\,\,\, \)\(= \,\,\left[ {4t\,\, - \,\,\frac{{0.08{t^2}}}{2}} \right]_0^{50}\,\, = \,\,100\,\,C\)
હવે, \({\text{Q = ne}}\) પરથી \(n\,\, = \,\,\frac{Q}{e}\,\, = \,\,\frac{{100}}{{1.6\,\, \times \,\,{{10}^{ - 19}}}}\,\, = \,\,6.25\,\, \times \,\,{10^{20}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રવાહ સ્ત્રોત સાથે પ્રથમ $R_1$ અવરોધના કોષને અને પછી $R_2$ અવરોધ સાથે જોડતા તેમાં સમાન સમયમાં સમાન ઉષ્મા ઉત્પન્ન થાય છે. તો સ્ત્રોતનો આંતરિક અવરોધ કેટલો હશે?View Solution
- 2કોષને $ 2\,Ω$ અવરોધ સાથે જોડતાં $0.5\, A $ અને $ 5\,Ω $ સાથે જોડતાં $0.25 \,A$ પ્રવાહ પસાર થાય છે,તો કોષનો $ emf$ કેટલા .............. $volt$ થાય?View Solution
- 3View Solutionનીચે આપેલા આકૃતિમાં દર્શાવેલ અવરોધોના નેટવર્ક માટે સાચો વિકલ્પ પસંદ કરો.
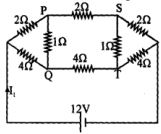
- 4આપેલ પરિપથને બેટરીમાંથી મળતો કુલ પ્રવાહ કેટલા .............. $A$ હશે?View Solution
- 5તારમાંથી વહેતો વિદ્યુત પ્રવાહ સમયના વિધેય તરીકે સમીકરણ $I=I_0+\beta t$ મુજબ બદલાય છે, જ્યા $I_0=20 \mathrm{~A}$ અને $\beta=3 \mathrm{~A} / \mathrm{s}$. તારના વિભાગમાંથી $20 \mathrm{~s}$ માંથી પસાર થતા વીજભારનો જથ્થો________છે.View Solution
- 6બે વિધુત બલ્બ જેમના અવરોધોનો ગુણોત્તર $1 : 2$ છે. તેમને સમાંતરમાં જોડી અચળ વોલ્ટેજ આપેલ છે તો તેમાં વ્યય થતા પાવરનો ગુણોત્તર .. હશે.View Solution
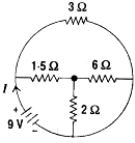
- 7આપેલ તંત્રમાં $4\, \Omega$ આંતરિક અવરોઘ ઘરાવતી બેટરીમાંથી મહતમ પાવર મેળવવા માટે $R $ નું કેટલા ............. $\Omega$ હોવું જોઈએ?View Solution
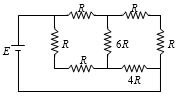
- 8આપેલ પરિપથને $3\, volt$ અને અવગણ્ય આંતરિક અવરોધ ધરાવતી બેટરી સાથે જોડેલ છે. તો તેમાંથી પસાર થતો પ્રવાહ $I$ કેટલા $A$ નો હશે?View Solution
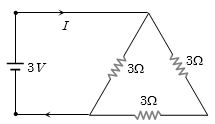
- 9View Solutionજ્યારે મલ્ટીમીટર (અવરોધ માપવાના મોડમાં કાર્ય કરે) પ્રોબને એક ઘટક સાથે જોડેલ હોય, તેને માત્ર ઊલટું કરતાં નીચેનામાંથી કયું અવલોકન કરવામાં આવશે નહિ?
- 10$4 \,mm$ ત્રિજ્યા ધરાવતા નળાકારીય તારમાં પ્રવાહ ધનતા તેના આડછેદને સમાંતર નિયમિત છે, અને તે $4 \times 10^{6} \,Am ^{-2}$ જેટલી છે. તારના બહારના ભાગમાં $\frac{R}{2}$ અને $R$ ની વરચે ત્રિજ્યાવર્તી અંતરમાંથી પસાર થતો પ્રવાહ .......... $\pi A$ હશે.View Solution