એક બોલને $u$ વેગ સાથે શિરોલંબ ઊર્ધ્વ દિશામાં ઊછાળવામાં આવે છે, ઉપરની ગતિની છેલ્લી $t$ સેકન્ડમાં બોલે કાપેલું અંતર કેટલું હશે?
AIPMT 2003, Medium
Download our app for free and get started
a
(a) The distance covered by the ball during the last $t$ seconds of its upward motion = Distance covered by it in first $t$ seconds of its downward motion
(a) The distance covered by the ball during the last $t$ seconds of its upward motion = Distance covered by it in first $t$ seconds of its downward motion
From$h = ut + \frac{1}{2}g\,{t^2}$
$h = \frac{1}{2}g\;{t^2}$ [As $u = 0$ for it downward motion]
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ટાવરની ટોચ પરથી મુકત કરવામાં આવેલ પદાર્થ છેલ્લી બે સેકન્ડમાં $40\;m$ જેટલું અંતર કાપે છે. આ ટાવરની ઊંચાઈ ($m$ માં) કેટલી હશે?View Solution
- 2View Solutionનીચેનામાંથી કયો ગ્રાફ અચળ પ્રવેગી ગતિનો છે
- 3$45\, km/hr$ ની ઝડપથી ગતિ કરતી પોલીસની કાર $153\, km/hr$ ની ઝડપથી ગતિ કરતી ચોરની કારની પાછળ છે.પોલીસ $180\, m/s$ ની ઝડપથી ગોળી છોડે છે.ગોળી ચોરની કારને કેટલા.......$m/s$ ઝડપથી અથડાશે?View Solution
- 4બે કાર $A$ અને $B$ સમાન દિશામાં $30 \,m / s$ અને $20 \,m / s$ વેગ સાથે ગતિ કરી રહી છે. જ્યારે કાર $A$ એ કાર $B$ ની પાછળ $d$ અંતરે હોય ત્યારે, કાર $A$ નો ડ્રાઈવર બ્રેક મારીને $2\, m / s ^2$ નો એકસમાન પ્રતિપ્રવેગ ઉત્પન કરે છે. જ્યારે બંને કાર વચ્ચે કોર અથડામણ નહી થાય ત્યારે,View Solution
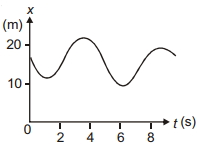
- 5આકૃતિ એ સમયના કાર્ય તરીક $x$- અક્ષ પર ગતિ કરી રહેલા કણોની સ્થિતિ બતાવે છેView Solution
- 6$A $ પદાર્થ $a_1$ પ્રવેગથી સ્થિર સ્થિતિમાંથી ગતિ શરૂ કરે છે,અને $2 sec$ પછી $B$ પદાર્થ $a_2$ પ્રવેગથી સ્થિર સ્થિતિમાંથી ગતિ શરૂ કરે છે.જો બંનએ $5^{th}\, sec$ માં કાપેલ અંતર સમાન હોય તો ${a_1}:{a_2}=$View Solution
- 7એ કે કાર સુરેખ રેખા પર ગતિ કરે છે. જેમકે આકૃતિમાં $OP$. આ કાર $18\; s$ માં $O$ થી $P$ જાય છે અને $6\; s$ માં $P$ થી $Q$ પરત જાય છે. કાર $O$ થી $P$ જાય ત્યારે તેનો સરેરાશ વેગ અને સરેરાશ ઝડપ શું હશે ?View Solution
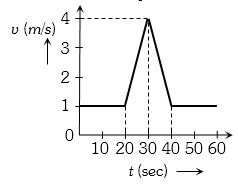
- 8એક પદાર્થનો વેગ વિરુધ્ધ સમયનો આલેખ આપેલ છે. તો પદાર્થે કાપેલું અંતર($m$ માં) પ્રવેગ અશૂન્ય હોય,તે સમયની વચ્ચે કેટલું થશે?View Solution
- 9એક ટ્રેન $60 km/hr$ ની ઝડપથી પ્રથમ કલાક અને $40 km/hr$ ની ઝડપથી અડધો કલાક ગતિ કરે ,તો સરેરાશ ઝડપ કેટલા..........$km/h$ થાય?View Solution
- 10ટાવરની ટોચથી $10 \,m / s$ ની ઝડપે બોલ ઉપરની તરફ ફેકવામાં આવે છે અને તે $20 \,m / s$ ની ઝડપ સાથે જમીન પર પહોંચે છે. ટાવરની ઉંચાઈ ............ $m$ થાય? [$g = 10 \,m / s ^2$ લો]View Solution