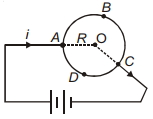
એક એેકરૂપ વર્તુળાકાર રીંગને બેટરીના છેડા સાથે જોડેલ છે.તારના $A B C$ ભાગને લીધે કેન્દ્ર પાસે ચુંબકીયક્ષેત્ર પ્રેરણ કેટલુ હશે? ($ABC$ની સંજ્ઞા, $=I_1$ ની $A D C$ લંબાઈ $\left.=I_2\right)$

Medium
a
(a)
(a)
Let current in part \(A B C\) is \(i_1\) and in part \(A D C\) is \(i_2\)
\(i=\frac{i l_2}{l_1+l_2}\) (As \(A B C\) and \(A D C\) part are in parallel connection) and subtended by \(A B C\) at centre \(O\) will be \(=\left(\frac{2 \pi}{l_1+l_2}\right)\left(l_1\right)\)
so using \(B=\frac{\mu_0 i}{2 a}\left(\frac{\theta}{2 \pi}\right)\)
\(B=\frac{\mu_0}{2 R}\left(\frac{i l_2}{l_1+l_2}\right) \frac{2 \pi}{\left(l_1+l_2\right)} \frac{\left(l_1\right)}{2 \pi}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$100 \Omega$ નો અવરોધ ધરાવતા ગેલ્વેનોમીટરને હ્યારે $400 \Omega$ ના અવરોધ સાથે શ્રેણીમાં જોડવામાં આવે છે ત્યારે $10 \mathrm{~V}$ સુધીનો વૉલ્ટેજ માપે છે . ગેલ્વેનોમીટર ને $10$ $A$ જેટલો પ્રવાહ માપી શકે તેવા એમીટરમાં રૂપાંતારિત કરવા માટેનો જરૂરી અવરોધ $x \times 10^{-2} \Omega$ છે. $x$ નું મૂલ્ય. . . . . . . . હશે.View Solution
- 2$q$ વિદ્યુતભાર અને $m$ દળ ધરાવતો કણ $x-$ અક્ષની દિશામાં $v$ વેગથી ગતિ કરે છે.તો કઇ આકૃતિમાં કણ પર લાગતું બળ શૂન્ય થાય?View Solution
- 3અર્ધઆવર્તન પ્રક્રિયાનો ઉપયોગ કરીને ગેલ્વેનોમીટરનો અવરોધ શોધવાના પરિપથમાં $6\,V$ ની બેટરી અને $11\,k\Omega $ ના ઊંચા અવરોધનો ઉપયોગ કરવામાં આવે છે.તેની પ્રવાહ સંવેદિતા $60\,\mu A/$કાંપા છે. શંટની ગેરહાજરીમાં જ્યારે પ્રવાહ વહેતો હોય ત્યારે ગેલ્વેનોમીટરનું આવર્તન $\theta = 9$ છે. $\theta /2$ આવર્તન મેળવવા માટે કેટલા $\Omega$ ના શંટની જરૂર પડે?View Solution
- 4એક વર્તુળાકાર વિદ્યુતપ્રવાહધારિત ગુંચળાની ત્રિજ્યા $R$ છે. ગુંચળાના કેન્દ્રથી તેની અક્ષ પર કેટલા અંતરે ચુંબકીયક્ષેત્રની તીવ્રતા તેના કેન્દ્ર પરની તીવ્રતા કરતા $\frac{1}{2 \sqrt{2}}$ ગણી હશે?View Solution
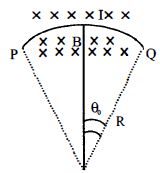
- 5ચુંબકીયક્ષેત્ર $B$ (કાગળના સમતલને લંબ $\times \times \times $ વડે દર્શાવેલ છે) માં એક તારને $R$ ત્રિજયા ધરાવતી ચાપ તરીકે $P$ અને $Q$ બિંદુ વચ્ચે જડિત કરેલ છે. જેમાંથી પ્રવાહ $I$ પસાર થાય છે. તો તારથી બનેલ ચાપ કેન્દ્ર સાથે $2\theta_0$ નો ખૂણો બનાવતી હોય તો તારમાં તણાવ કેટલું હશે?View Solution
- 6$10^{-2} \,kg$ દળ ધરાવતા કણ પર $5 \times 10^{-8} \,C$ વિદ્યુતભાર છે. કણને $10^5 \,m/s $ ના સમક્ષિતિજ વેગથી વિદ્યુતક્ષેત્ર $E$ અને ચુંબકીયક્ષેત્ર $B$ માં ગતિ કરે છે. કણને સમક્ષિતિજ દિશામાં ગતિ શરૂ રાખવા માટે જરૂરી છે કેView Solution
$(1)$ $ B$ વેગને લંબ અને $E $ વેગની દિશામાં હોવું જોઇએ.
$(2) $ $B$ અને $E $ વેગની દિશામાં હોવું જોઇએ.
$(3)$ $B$ અને $E $ પરસ્પર લંબ હોવા જોઇએ અને બંને વેગની દિશાને લંબ હોવા જોઇએ.
$(4)$ $B $ વેગની દિશામાં હોવું જોઇએ અને $E$ વેગની દિશાને લંબ હોવું જોઇએ.
આપેલામાંથી કયા વિધાનની જોડી શક્ય છે?
- 7View Solutionપૂર્વ તરફ ગતિ કરતો એક ઘન વિદ્યુતભારિત થયેલ કણ એક ઉપરની દિશામાં પ્રવર્તતા ચુંબકીય ક્ષેત્રમાં પ્રવેશે છે. તો કણ....
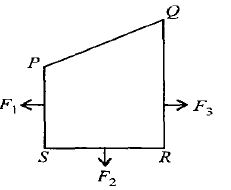
- 8પ્રવાહધારીત એક બંધ લૂપ $PQRS$ ને એકસમાન ચુંબકીયક્ષેત્રમાં મૂકવામાં આવેલ છે. જો $PS, SR$ અને $RQ$ બાજુ પર ચુંબકીય બળ $F _{1}, F _{2}$ અને $F _{3}$ હોય અને કાગળના સમતલમાં અને દર્શાવેલ દિશામાં હોય, તો $QP$ બાજુ પર લાગતું બળ કેટલું હશે?View Solution
- 9View Solutionજો સમાન વેગમાન ધરાવતો ઇલેક્ટ્રોન અને પ્રોટોન ચુંબકીયક્ષેત્રને લંબ પ્રવેશે, તો ...
- 10$r$ ત્રિજ્યાની એક વર્તુળાકાર સુવાહક રીંગમાંથી અચળ વિદ્યુતપ્રવાહ $i$ પસાર થાય છે. તેને એકરૂપ ચુંબકીય ક્ષેત્ર $B$માં મૂકવામાં આવ્યો છે કે જેથી $B$ રિંગના સમતલને લંબ છે. રીંગ પર લાગતું કુલ ચુંબકીય બળ કેટલું છે ?View Solution
