ધારો કે, \(m\) દળના બ્લોકની ઝડપ \( v \) અને \(M \) દળના બ્લોકની ઝડપ \(V\) છે.
અહીં, (બ્લોક + સ્પ્રિંગ) ના તંત્રને ધ્યાનમાં લેતાં યાંત્રિક ઊર્જા અને વેગમાન નું સંરક્ષણ થશે.
યાંત્રિક ઊર્જાના સંરક્ષણના નિયમ અનુસાર, પ્રારંભિક યાંત્રિક ઊર્જા = અંતિમ યાંત્રિક ઊર્જા
\(\therefore \,\frac{1}{2}K{x^2} = \frac{1}{2}M{\upsilon ^2} + \frac{1}{2}M{V^2}\,\,\,...\,...\,...(1)\)
હવે, વેગમાનના સંરક્ષણના નિયમ અનુસાર, પ્રારંભિક વેગમાન = અંતિમ વેગમાન
\(\therefore MV - m\upsilon \, = \,0\,\,\,\,\therefore \,V = \frac{{m\upsilon }}{M}\,\,\,...\,\,\,...\,\,...\,\,(2)\)
\(V \) ની આ કિંમત સમીકરણ \((1)\) માં મુકતાં,
\(\frac{1}{2}K{x^2}\, = \,\frac{1}{2}m{\upsilon ^2} + \frac{1}{2}M{\left( {\frac{{m\upsilon }}{M}} \right)^2}\,\,\,\therefore \,K{x^2}\, = \,m{\upsilon ^2}\left[ {1 + \frac{m}{M}} \right]\,\,\, = \,m{\upsilon ^2}\left[ {\frac{{M + m}}{M}} \right]\,\,\,\,\)
\(\therefore {\upsilon ^2}\, = \,\frac{{K{x^2}M}}{{m(M + m)}}\,\,\,\,\,\,\therefore \,\,\,\upsilon \, = \,\sqrt {\frac{{KM}}{{m(M + m)}}} \,\, \cdot \,\,x\,\,\,\,\,\)
\(v\) ની કિંમત સમીકરણ \((2) \) માં મુકતાં,
\(V\, = \,\frac{m}{M}\, \cdot \sqrt {\frac{{KM}}{{m(M + m)}}} \, \cdot x\,\,\,\, = \,\sqrt {\frac{{mK}}{{M(M + m)}}} \, \cdot x\)
Download our appand get started for free
Similar Questions
- 1View Solutionવિધાન: બે બિલિયર્ડ દડાના સ્થિતિસ્થાપક સંઘાત માં ટૂંકાગાળાના દોલન દરમિયાન (જ્યારે તેઓ સંપર્કમાં હોય ત્યારે) કુલ ગતિઉર્જાનું સંરક્ષણ થાય છે.
કારણ: ઘર્ષણ વિરુદ્ધ વપરાયેલ ઉર્જા એ ઉર્જા સંરક્ષણના નિયમ ને અનુસરતી નથી.
- 2$H$ ઊંચાઈ પરથી મુકત પતન કરતો એક પદાર્થ, $h$ ઊંચાઈ પર આવેલા એક ઢોળાવ વાળા સમતલ સાથે સંપૂર્ણ સ્થિતિસ્થાપક રીતે અથડાય છે. અથડામણ બાદ પદાર્થનો વેગ સમક્ષિતિજ થાય છે. જો આ પદાર્થ જમીન પર પહોંચવા માટે મહત્તમ સમય લેતો હોય તો $\frac{\mathrm{H}}{\mathrm{h}}$ નું મૂલ્ય .....View Solution
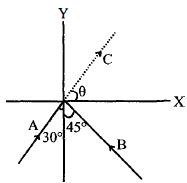
- 3સમાન દળ $M$ ધરાવતા બે કણ $A$ અને $B$ સમાન ઝડપ $v$ થી આકૃતિ માં દર્શાવ્યા મુજબ ગતિ કરે છે. તેઓ સંપૂર્ણ અસ્થિતિસ્થાપક સંઘાત પામીને એક કણ $C$ તરીકે ગતિ કરે છે.તો કણ $C$ ના પથ દ્વારા $X-$ અક્ષ સાથે બનાવેલ ખૂણો $\theta $ શેના દ્વારા દર્શાવી શકાય ?View Solution
- 4$2m$ લંબાઇની ચેઇન ટેબલ પર $60cm$ લંબાઇ લટકતી હોય,તેવી રીતે પડેલ છે.જો ચેઇનનું દળ $4 \,kg$ હોય,તો ચેઇનને ટેબલ પર લાવવા કેટલા .............. $\mathrm{J}$ કાર્ય કરવું પડે?View Solution
- 5બળ ક્ષેત્ર $\vec{F}$ માટે સ્થિતિમાન ઊર્જા $U(x, y)=\cos (x+y)$ વડે દર્શાવાય છે. $(0, \pi / 4)$ પર રહેલા કણ પર લાગતું બળ.View Solution
- 6$9 kg$ દળનો એક બોમ્બ $3 kg$ અને $6 kg$ દળના બે ટુકડાઓમાં વિસ્ફોટ પામે છે. $6 kg $ ના ટુકડાની ગતિ ઊર્જા $120 J$ તો $3 kg$ દળની ગતિ ઊર્જા ......... $J$ શોધો.View Solution
- 7એક પદાર્થને જમીનથી $h$ ઊંચાઈ એ થી મુક્ત કરવામાં આવે છે. જેટલી વાર તે જમીન પર અથડાય ત્યારે તે તેની ગતિઉર્જા ના $50\%$ જેટલી ગતિઉર્જા ગુમાવે છે. તો $t \to \infty $ દરમ્યાન તેણે કાપેલ અંતર કેટલું હશે?View Solution
- 8$r$ ના વિધેયમાં સ્થિતિ ઊર્જા $U=\frac{A}{r^{10}}-\frac{B}{r^{5}}$ વડે આપવામાં આવે છે, જેમાં $r$ એ આંતરપરમાણીય અંતર, $A$ અને $B$ ધન અચળાંકો છે. બે પરમાણુ વચ્ચેનું સંતુલન અંતર...... હશે.View Solution
- 9$200gm$ અને $ 400 gm $ દળ ધરાવતા રબરના બે દડા $ A$ અને $ B$ વિરુધ્ધ દિશામાં ગતિ કરે છે.$A$ દડાનો વેગ $0.3 m/s $ છે,અથડામણ પછી બંને દડા સ્થિર થઇ જતાં હોય,તો $ B $ દડાનો વેગ કેટલા ................ $\mathrm{m} / \mathrm{s} $ થશે?View Solution
- 10જયારે સ્પિંગ્રને $2 cm$ ખેંચતાં $100 J$ ઊર્જાનો સંગ્રહ થાય છે.હવે,તેને ફરીથી $2 cm$ ખેંચતા ઊર્જામાં કેટલા ............ $\mathrm{J}$ વધારો થશે?View Solution
