From \(Newton's\,law\) of cooling,
\(t = \frac{1}{k}{\log _e}\left( {\frac{{{\theta _2} - {\theta _0}}}{{{\theta _1} - {\theta _0}}}} \right)\)
From question and above equation,
\(5 = \frac{1}{k}{\log _e}\frac{{\left( {40 - 30} \right)}}{{\left( {80 - 130} \right)}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( 1 \right)\)
\(And,t = \frac{1}{k}{\log _e}\frac{{\left( {32 - 30} \right)}}{{\left( {62 - 30} \right)}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( 2 \right)\)
Dividing equation \((2)\) by \((1)\),
\(\frac{t}{5} = \frac{{\frac{1}{k}{{\log }_e}\frac{{\left( {32 - 30} \right)}}{{\left( {62 - 30} \right)}}}}{{\frac{1}{k}{{\log }_e}\frac{{\left( {40 - 30} \right)}}{{\left( {80 - 30} \right)}}}}\)
On solving we get, time taken to cool down from \({62^ \circ }C\,to\,{32^ \circ }C,\)
\(t=8.6\,minutes.\)
Download our appand get started for free
Similar Questions
- 1સ્થાયી ઉષ્મા અવસ્થામાં રહેલો ધાતુનો સળિયો તેના એક છેડેથી બીજા છેડે ઉષ્માનું વહન કરે છે. સળિયાના ગરમ છેડાથી $x$ લંબાઈ મુજબ તેના તાપમાન $\theta$ માં થતા ફેરફરરનો આલેખ નીચેનામાંથી કેવો હશે?View Solution
- 2$227^{\circ} C$ તાપમાન , $2\;m$ ત્રિજ્યા અને $0.8$ ઉત્સર્જક્તા ધરાવતા ગોળાનો ઉત્સર્જન પાવર ($W$ માં) કેટલો હોય?View Solution
- 3View Solutionજો સૂર્યનું (કાળો પદાર્થ) તાપમાન બમણું થાય, તો પૃથ્વી દ્વારા મેળવાતી ઊર્જા વધીને કેટલા ગણી થાય?
- 4View Solutionવિનના નિયમ અનુસાર....
- 5કાળો પદાર્થ $2880\;K$ તાપમાને છે.આ પદાર્થ તરંગલંબાઈ $499\;nm$ થી $500\;nm$ ની વચ્ચે ${U_1}$ ઉર્જાનું ઉત્સર્જન $999\;nm$ થી $1000\;nm$ ની વચ્ચે ${U_2}$ ઉર્જાનું ઉત્સર્જન અને $1499\;nm$ થી $1500\;nm$ ની વચ્ચે ${U_3}$ ઉર્જાનું ઉત્સર્જન કરે તો..... (વીનનો અચળાંક $b = 2.88 \times {10^6}\;nm\,K$).View Solution
- 6ગોળો, સમઘન અને પાતળી ગોળાકાર પટ્ટીએ સમાન પદાર્થની બનેલી છે તે $200^{\circ} C$ જેટલા તાપમાને ગરમ કરવામાં આવે તો એમાંથી ક્યો પદાર્થ ધીમેથી ઠંડો પડશે, જો રૂમ તાપમાને રાખવામાં આવે ત્યારે ?View Solution
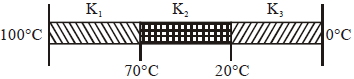
- 7ત્રણ સમાન આડછેદ અને લંબાઈ ધરાવતા સળિયાને જુદા-જુદા દ્રવ્યમાંથી બનાવેલ છે જેમની ઉષ્માવાહકતા અનુક્રમે $K _{1}, K _{2},$ અને $K _{3}$ છે. તેને પછી આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે સળિયાના એક છેડાને $100^{\circ} C$ તાપમાને અને બીજા છેડાને $0^{\circ} C$ તાપમાને રાખેલ છે જો સંતુલન સમયે સળીયાના જોડાણના જંકશનનું તાપમાન અનુક્રમે $70^{\circ} C$ અને $20^{\circ} C$ હોય અને સળિયાની સપાટી પરથી કોઈ પણ ઉર્જાનો વ્યય થતો ના હોય તો $K _{1}, K _{2}$ અને $K _{3}$ વચ્ચેનો સંબધ શું હશે?View Solution
- 8$50 cm$ લંબાઈ અને $5 cm^{2}$ આડછેદના ક્ષેત્રફળમાંથી ઉષ્માનું વહન થાય છે. તેના છેડાઓ અનુક્રમે $25 °C$ અને $125°C$ છે. સળિયાના પદાર્થની ઉષ્માવાહકતા $0.092\, kcal/ms \,C$ સળિયાનો તાપમાન પ્રચલન ....... $^oC/cm$ છે.View Solution
- 9ત્રણ જુદા જુદા તારાઓ $P, Q$ અને $R$ ના પ્રકાશના અભ્યાસ પરથી જાણવા મળ્યું કે પ્રકાશના $P$ ના વર્ણપટમાં જાંબલી રંગની તીવ્રતા મહત્તમ, $R$ ના વર્ણપટમાં લીલા રંગની તીવ્રતા મહત્તમ અને $Q$ ના વર્ણપટમાં લાલ રંગની તીવ્રતા મહત્તમ છે. જો $P, Q$ અને $R$ ના નિરપેક્ષ તાપમાન અનુક્રમે $T_P , T_Q$ અને $T_R$ હોય, તો ઉપરોક્ત અવલોકનો પરથી તે તારણ કાઢી શકાય છે કેView Solution
- 10View Solutionજ્યારે સળીયાના બે છેડાઓ પર રૂ વીંટાળીને જુદાં જુદાં તાપમાને રાખેલ છે અને અમુક સમય બાદ સળિયાનું દરેક બિંદુ અચળ તાપમાન છે, ત્યારે.....
