When body rolls dawn on inclined plane with velocity \(V_0\) at bottom then body has both rotational and translational kinetic energy.
Thereforce, by law of conservation of energy,
\(\begin{array}{l}
P.E\, = \,K.{E_{trans}} + K.{E_{rotational}}\\
= \frac{1}{2}mV_0^2 + \frac{1}{2}I{\omega ^2}\\
= \frac{1}{2}mV_0^2 + \frac{1}{2}m{k^2}\frac{{V_0^2}}{{R_0^2}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {I = m{k^2},\omega = \frac{V}{{{R_0}}}} \right]
\end{array}\)
When body is sliding down then body has only translatory motion.
\(\begin{array}{l}
\therefore P.E = K.{E_{trans}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}m{\left( {\frac{5}{4}{v_0}} \right)^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)
\end{array}\)
Dividing \((i)\) by \((ii)\) we get
\(\begin{array}{l}
\frac{{P.E}}{{P.E}} = \frac{{\frac{1}{2}mv_0^2\left[ {1 + \frac{{{K^2}}}{{R_0^2}}} \right]}}{{\frac{1}{2} \times \frac{{25}}{{16}} \times mV_0^2}}\\
= \frac{{25}}{{16}} = 1 + \frac{{{K^2}}}{{R_0^2}} \Rightarrow \frac{{{K^2}}}{{R_0^2}} = \frac{9}{{16}}\\
or,\,\,\,K = \frac{3}{4}\,{R_{0.}}
\end{array}\)
Download our appand get started for free
Similar Questions
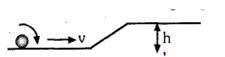
- 1ઘનગોળો ઘર્ષણ રહિત સપાટી પર રોલિંગ કરે છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે સ્થાનાંતરીત વેગ $v\ \ m/s$ થી ગતિ કરીને ઢોળાવ વાળા સમતલ પર ચઢે છે. ત્યારે $v$ કેટલું હોવું જોઈએ ?View Solution
- 2$x-$ અક્ષ પર ત્રણ દળ મૂકવામાં આવ્યા છે: $300 \,g$ ઉગમબિંદુ પર, $500\,g$ એ $x=40 \,cm$ પર અને $400\,g$ એ $x =70\,cm$ પર છે. ઉગમબિંદુથી દ્રવ્યમાનકેન્દ્રનું અંતર ($cm$ માં) કેટલું હશે?View Solution
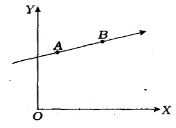
- 3$m$ દળનો એક કણ $XY$ સમતલમાં $AB$ સીધા માર્ગે $v$ વેગથી ગતિ કરે છે. સંદર્ભબિંદુ $O$ ને અનુલક્ષીને $A$ બિંદુએ કણનું કોણીય વેગમાન $L_A $ અને $B$ બિંદુએ $L_B$ હોય, તો ........View Solution
- 4$M$ દળની વર્તૂળાકાર તકતીનો પ્રારંભિક વેગ $\omega_1$ છે. બે નાના $ m $ દળના ગોળાઓને તકતીના વ્યાસના વિરૂદ્ધ બિંદુઓ પર જોડેલા છે. તકતીનો અંતિમ કોણીય વેગ શું થશે ?View Solution
- 5$60 \,kg$ દળનો એક માણસ $140 \,kg$ દળ ની એક બોટ પર ઊભો છે કે જે શાંત પાણી માં સ્થિર સ્થિતિમાં છે. તે વ્યક્તિ કાંઠા થી $20\,m$ દૂર છે. તે માણસ કાંઠા તરફ $1.5 \,m / s$ ની અચળ ઝડપે $4 \,s$ સુધી ચાલવાનું શરુ કરે છે. તેનું કાંઠા થી અંતિમ અંતર .............. $m$ હશે.View Solution
- 6એક સળિયાની તેના દ્રવ્યમાનકેન્દ્રમાંથી પસાર થતી તેને લંબ એવી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{1}{{12}}M{L^2}$ છે. હવે સળિયાને મધ્યમાંથી એવી રીતે વાળવામાં આવે છે કે જેથી બનતા બે ભાગ તે જ સમતલમાં નો ખૂણો બનાવે છે. તો આ તંત્રની તે જ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
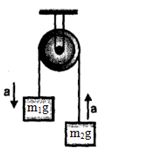
- 7$m_1$ અને $m_2$ દળ ધરાવતા બે પદાર્થને વજન રહિત દોરીના છેડે આકૃતિમાં દર્શાવ્યા મુજબ ગરગડી પરથી લટકાવેલ છે. $m_2 < m_1$ ગરગડી ઘર્ષણ રહિત અને વજન રહિત છે. આ બે પદાર્થથી બનતા તંત્રના દ્રવ્યમાન-કેન્દ્રનો પ્રવેગ.....View Solution
- 8$(a)$ એક પદાર્થ નું ગુરૂત્વ કેન્દ્ર એક એવું બિંદુ છે કે જ્યાં પદાર્થનું વજન લાગતું હોય.View Solution
$(b)$ જો પૃથ્વીને અનંત મોટી ત્રિજ્યા ધરાવતી માનવામાં આવે તો દ્રવ્યમાન કેન્દ્ર એ ગુરૂત્વ કેન્દ્રની સાથે સંપાત થાય છે.
$(c)$ કોઈ બાહ્ય બિંદુ પર કોઈપણ પદાર્થને લીધે ગુરુત્વાર્કર્ષણ ક્ષેત્રની તીવ્રતાને માપવા માટે પદાર્થનું સમગ્ર દળ તેના ગુરુત્વ કેન્દ્ર પર કેન્દ્રિત થયેલું ગણી શકાય.
$(d)$ એક અક્ષને અનુલક્ષીને ભ્રમણ કરતાં કોઈપણ પદાર્થની ચક્રાવર્તન ત્રિજ્યા એ ગુરૂત્વ કેન્દ્રમાંથી દોરવામાં આવતા લંબની લંબાઈ છે.
નીચેનામાંથી વિધાનોની કઈ જોડ સાચી છે?
- 9$1\,kg$ દળની વસ્તુનો સ્થાન સદિશ $\overrightarrow{ r }=(3 \hat{ i }-\hat{ j }) \,m$ અને તેનો વેગ $\overrightarrow{ v }=(3 \hat{ j }+\hat{ k }) \,ms ^{-1}$ છે. કોણીય વેગમાનનું મૂલ્ય $\sqrt{x} \,Nm$ મળે છે તો $x$ નું મૂલ્ય ............ હશે.View Solution
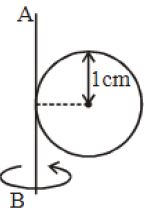
- 10$5\,g$ દળ અને $1\,cm$ ત્રિજ્યા ધરાવતો એક ધાતુનો સિક્કો એક પાતળી નહિવત દળ ધરાવતા તાર સાથે આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડેલો છે તંત્ર શરૂઆતમાં સ્થિર છે. અચળ ટોર્ક લગાવતા તંત્ર $AB$ ની સાપેક્ષે $25$ પરિભ્રમણ $5\,s$ માં પૂર્ણ કરતું હોય તો આ ટોર્ક કેટલું હશે?View Solution