આ પરિસ્થિતિ આકૃતિમાં દોરેલી છે. પ્રકાશ શિરોલંબ બાજુ \(BC\) માંથી નિર્ગમન પામશે નહીં.
જો \( i > \theta_c\) અથવા \(sin\,\, i > sin\,\, \theta_c\)
\(\sin \,\,i\,\,\, > \,\,\,\frac{1}{\mu }\,\,\,\left[ {as\,\,\,\sin {\theta _c} = \,\,\frac{1}{\mu }} \right]\,\,\,\,......\,\,\,(i)\)
O પાસે સ્નેલના નિયમ પરથી \(1 × sin \theta = \mu \,\, sin r \)
\(\Delta \,\, OPR\) માં ,\( r + 90 + i = 180\) \( r + i = 90°\)
તેથી \(\,sin\,\theta \,\, = \,\,\mu \,\,sin\,\,(90 - i)\,\, = \,\,\mu \,\,cos \,\,i\,\,\,\, \Rightarrow \,\, cos \,i\,\,\, = \, \frac{{sin\theta }}{\mu }\)
તેથી \(sin\,i\,\, = \,\,\,\sqrt {1 - co{s^2}i} \,\,\, = \,\,\,\sqrt {1 - {{\left[ {\frac{{\sin \theta }}{\mu }} \right]}^2}} \,\,\,......\,\,\,(ii)\)
તેથી \(sin\,\, i\) નું મૂલ્ય સમીકરણ \((ii)\) માંથી \( (i)\) માં મૂકતાં,
\(\sqrt {1 - \frac{{{{\sin }^2}\theta }}{{{\mu ^2}}}} \,\,\, > \,\,\frac{1}{\mu }\,\,\,i.e.,\,\,\,{\mu ^2} > \,\,\,1\,\, + \,\,{\sin ^2}\theta \,\,\,\therefore \,\,\,\,{\mu ^2} > 2\,\,\,\,\,\,\)
\(\because \,\,\,{({\sin ^2}\theta )_{\max }} = \,\,\,1\,\,\)
\(\, \Rightarrow \,\,\mu \,\, > \,\,\,\sqrt 2 \,\,\,\,\,\therefore \,\,{\mu _{\min }} = \,\,\sqrt 2 \)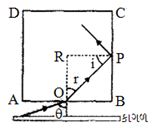
Download our appand get started for free
Similar Questions
- 1$f$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાના ધ્રુવ પાસે સૂર્ય (વ્યાસ $d$) $\theta$ રેડિયન ખૂણો આંતરે છે. તો અરીસાની વડે રચાતા સૂર્યના પ્રતિબિંબનો વ્યાસ..... હશે.View Solution
- 2$A$ પ્રિઝમકોણ ધરાવતા પ્રિઝમની એક બાજુ પર ચાંદી લગાવેલ છે. એક બાજુ પર $2A$ ખૂણે કિરણ આપાત કરતાં ચાંદી લગાવેલ બાજુ પર પરાવર્તન પામીને મૂળ માર્ગે પાછું આવે છે. પ્રિઝમના પદાર્થનો વક્રીભવનાંક $\mu$ કેટલો હશે?View Solution
- 3$\frac {4}{3}$ વક્રીભવનાંક ધરાવતા પાણીમાં $12\,cm$ ઊંડાઈએ માછલીને બહાર દેખાતું ક્ષેત્રફળની ત્રિજ્યા ......... $cm$.View Solution
- 4પ્રિઝમકોણ $A=1^{\circ}$ અને વક્રીભવનાંક $\mu=1.5 .$ ધરાવતા પ્રિઝમ નો લઘુતમ વિચલન કોણ $N/10$ હોય તો $N$ .........View Solution
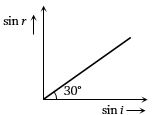
- 5માધ્યમ માટે વક્રીભૂતકોણ $(sin r)$ અને આપાતકોણ($sin i)$ નો આલેખ આપેલ છે,જો માધ્યમમાં પ્રકાશની ઝડપ $nc$ હોય,તો $n=$ ____View Solution
- 6View Solutionમાણસની આંખનું નજીકત્તમ અને દૂરનું બિંદુ .......છે.
- 7એક પ્રકાશનું કિરણ પ્રિઝમની વક્રીભૂત સપાટી પર $\theta$ કોણે આપાત થાય છે અને લંબ રીતે બીજી બાજુ પરની નિર્ગમન પામે છે. જો પ્રિઝમ કોણ $5° $ હોય અને પ્રિઝમમાં દ્રવ્યનો વક્રીભવનાંક $1.5$ હોય, તો આપાત કોણ......$^o$View Solution
- 8$180 cm$ લંબાઇ ધરાવતા માણસ સમતલ અરીસાથી $1m $ અંતરે છે.માણસની આંખ માથાથી $10cm$ નીચે છે,તો અરીસાની લઘુત્તમ લંબાઇ કેટલા ......$cm$ હોવી જોઈએ કે જેથી માણસ પોતાનું આખું પ્રતિબિંબ જોઇ શકે?View Solution
- 9$1.5$ વક્રીભવનાંક ધરાવતા પાતળા પ્રિઝમનો લઘુત્તમ વિચલનકોણ $5^o $ હોય,તો પ્રિઝમકોણ કેટલા .......$^o$ હશે?View Solution
- 10એક માધ્યમ માટે ક્રાંતિકોણ $30^o $ હોય,તો તે માધ્યમમાં પ્રકાશનો વેગ કેટલો થાય?View Solution
