એક કાર $100m$ ત્રિજયાના વર્તુળાકાર પથ પર અચળ ઝડપથી ગતિ કરે છે. એક ભ્રમણ પૂરું કરવા માટે તે $62.8 s$ નો સમય લે છે. એક ભ્રમણ બાદ કારનો સરેરાશ વેગ અને સરેરાશ ઝડપ અનુક્રમે શું હશે?
AIPMT 2006, Medium
Download our app for free and get started
Distance travelled in one rotation $($lap$)=2 \pi r$
$\therefore$ Average speed $=\frac{\text { distance }}{\text { time }}=\frac{2 \pi r}{t}$
$ =\frac{2 \times 3.14 \times 100}{62.8}$
$=10\ m s^{-1}$
Net displacement in one lap $=0$
Averagy velocity $=\frac{\text { net displacement }}{\text { time }}=\frac{0}{t}=0 .$
$\therefore$ Average speed $=\frac{\text { distance }}{\text { time }}=\frac{2 \pi r}{t}$
$ =\frac{2 \times 3.14 \times 100}{62.8}$
$=10\ m s^{-1}$
Net displacement in one lap $=0$
Averagy velocity $=\frac{\text { net displacement }}{\text { time }}=\frac{0}{t}=0 .$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$x$ - અક્ષની સાપેક્ષે ગતિ કરી રહેલા કાણોની સ્થિતિ $x=10 t-2 t^2$ દ્વારા આપવામાં આવે છે. તે સમય $(t)$ ની ........... $s$ કિંમતે માટે થોડા સમય માટે સ્થિર થશે?View Solution
- 2એક ફુગ્ગો $1.25 \;m / s ^2$ ના પ્રવેગથી જમીન પરથી ઉંચે જાય છે. $8\; sec$ પછી એક પથ્થર કુગ્ગામાંથી છોડવામાં આવે છે, તો પથ્થર એ $\left[ g =10\; m / s ^2\right]$View Solution
- 3કણે $t$ સમયમાં કાપેલું અંતર $x$ એ $x = {\left( {t + 5} \right)^{ - 1}}$ સૂત્ર મુજબ બદલાય છે. કણનો પ્રવેગ શેના સમપ્રમાણમાં હશે?View Solution
- 4જમીનથી $5\; m$ ઊંચાઇ પર આવેલા નળમાંથી એકસરખા સમયના અંતરાલમાં ટીપાં પડે છે. ત્રીજું ટીપું નળમાંથી છૂટે ત્યારે પ્રથમ ટીપું જમીન પર પડે છે. આ સમયે બીજુ ટીપું જમીનથી કેટલી ઊંચાઈ ($m$ માં) પર હશે?View Solution
- 5એક કાર સ્થિર સ્થિતિમાંથી નિયમિત પ્રવેગથી ગતિ કરીને $20$ સેકન્ડમાં $144 \,km/h$ ની ઝડપ પ્રાપ્ત કરે છે. તો કારે કેટલુ અંતર ($m$ માં) કાપ્યું હશે?View Solution
- 6એક પેરાશૂટધારી કૂદી પડયા પછી ઘર્ષણરહિત અવસ્થામાં $50 \,m$ જેટલો નીચે આવે છે. ત્યારબાદ પેરેશૂટ ખોલતાં તે $2\, m/s^2$ ના પ્રતિપ્રવેગથી ગતિ કરે છે. તે જમીન પર $3 \,m/s$ ના વેગથી પહોંચે છે. તેણે કેટલી ઊંચાઇએથી ($m$ માં) કૂદકો માર્યો હશે?View Solution
- 7કણનો પ્રવેગ $OA, AB$ અને $BC$ પર અનુક્રમે કેટલો મળે?View Solution
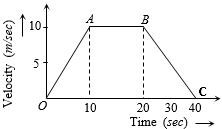
- 8એક ટ્રેન એક સીધા ટ્રેક પર $0.2 \,m / s ^2$ પ્રવેગ સાથે સ્ટેશનથી સ્થિર સ્થિતીમાં શરૂ થાય છે અને તે પછી પ્રતિપ્રવેગ $0.4\;m / s ^2$ ને કારણે સ્થિર થાય છે. તે અન્ય સ્ટેશન પર મહત્તમ ઝડપ પ્રાપ્ત થયા પછી સ્થિર થાય છે. જો કુલ લાગેલ સમય અડધો કલાક હોય, તો બે સ્ટેશનો વચ્ચેનું અંતર [ટ્રેનની લંબાઈને અવગણો] .......... $km$ થાય?View Solution
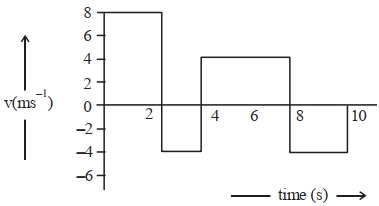
- 9સુરેખ ગતિ કરતા પદાર્થ માટે વેગ-સમયનો આલેખ આકૃતિમાં દર્શાવેલ છે. તો $0$ થી $10\,s$ ના સમય દરમિયાન સ્થાનાંતર અને પદાર્થે કાપેલ અંતરનો ગુણોત્તર ............ હોય.View Solution
- 10બે $A$ અને $B$ બોલને $180 \,m$ ઊંચા ટાવર ઉપર મૂકવામાં આવેલા છે. બોલ $A$ ને ટાવરની ટોચ પરથથી $t=0 \,s$ એ મુક્ત કરવામાં આવે છે. બોલ $B$ ને નીચે તરફ $u$ જેટલી પ્રારંભિક વેગ સાથે $t=2 \,s$ એ ફેકવામાં આવે છે. અમુક સમય બાદ, બંને બોલ જમીનથી ઉપર $100 \,m$ ઊંચાઈ આગળ મળે છે. $u$ નું મૂલ્ય ($ms ^{-1}$ માં) શોધો.View Solution
$\left[ g =10 \,ms ^{-2}\right.$ લો.$]$