એક કણ, $a$ ત્રિજયાના વર્તુળાકાર પથ પર આકર્ષિ સ્થિતિમાન $U = - \frac{k}{{2{r^2}}}$ અનુસાર ગતિ કરે છે.તેની કુલઊર્જા _______ થશે.
JEE MAIN 2018, Medium
b
\(F = \frac{{\partial u}}{{\partial r}}\,\hat r = \frac{K}{{{r^3}}}\,\hat r\)
\(F = \frac{{\partial u}}{{\partial r}}\,\hat r = \frac{K}{{{r^3}}}\,\hat r\)
Since particle is moving in circular path
\(\begin{gathered}
F = \frac{{m{v^2}}}{r} = \frac{K}{{{r^3}}} \Rightarrow m{v^2} = \frac{K}{{{r^2}}} \hfill \\
\therefore \,K.E. = \frac{1}{2}m{v^2} = \frac{K}{{2{r^2}}} \hfill \\
\end{gathered} \)
Total enerygy \(= P.E. + K.E.\)
\( = - \frac{K}{{2{r^2}}} + \frac{K}{{2{r^2}}} = zero\,\,\left( {\because \,P.E. = \frac{K}{{2{r^2}}}given} \right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$L $ લંબાઈ અને $M$ દળની એક સમાન શૃંખલા લીસા ટેબલની ધાર પર તેની ચોથા ભાગની લંબાઈ લટકતી રહે તેમ ગોઠવેલી છે. શૃંખલાના લટકતા ભાગને ઉંચકવા માટે જરૂરી કાર્ય શોધો.View Solution
- 2જયારે રબરબેન્ડને $x$ અંતરે ખેંચવામાં આવે છે,ત્યારે ઉત્પન્ન થતું પુન:સ્થાપક બળ $F=ax+bx^2$ છે,જયાં $a$ અને $b$ અચળાંક છે.જો રબરબેન્ડને તેની મૂળ સ્થિતિમાંથી $L$ અંતર ખેંચવામાં આવે તો થતું કાર્ય:View Solution
- 3View Solutionકણોના એેક તંત્ર અંદરની અંદર લાગતા આંતરિક બળો કોને બદલી શકે
- 4$\mathrm{m}$ દળના કણને સમક્ષિતિજ સાથે $\theta=\frac{\pi}{3}$ના ખૂણે $u$ વેગથી પ્રક્ષિપ્ત કરવામાં આવે છે. જ્યારે તે મહત્તમ ઊંચાઈ પર પહોચે ત્યારે તે બીજા સમાન દળ અને $u \hat i$ વેગ ધરાવતા કણ સાથે અસ્થિતિસ્થાપક સંઘાત અનુભવે છે.બંને ભેગા દળ જમીન પર આવે ત્યાં સુધી તેણે કેટલું સમક્ષિતિજ અંતર કાપ્યું હશે?View Solution
- 5$100 N/m$ બળ અચળાંક વાળી એક સ્પ્રિંગ $5 cm$ સુધી ખેંચાયેલી છે તો થતું કાર્ય શોધો.View Solution
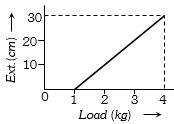
- 6સ્પિંગ્રની લંબાઇમાં થતા વધારા વિરુધ્ધ લટકાવેલ વજનનો આલેખ આપેલ છે. તો સ્પિંગ્રનો બળઅચળાંક ....... $ kg/cm$ થાય.View Solution
- 7View Solutionઊર્જા સંરક્ષણનો નિયમ શું નિર્દેંશ કરે છે?
- 8કોઇ પદાર્થની સ્થિતિ ઊર્જા $U = A - Bx^2$ છે. જ્યાં $x$ સ્થાનાંતર છે. તો પદાર્થ પર લાગતા બળનું મુલ્ય કેટલું હોય?View Solution
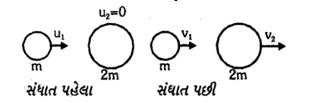
- 9એક બોલ સ્થિર સ્થિતિએ રહેલા તેના કરતા બમણું દળ ધરાવતા બોલ સાથે $1.5 m/s $ ના વેગથી હેેડઓન સંઘાત કરે છે. જો રેસ્ટીટ્યૂશન ગુણાંક $0.6$ હોય તો અથડામણ પછી તેઓનો વેગ કેટલો હશે ?View Solution
- 10View Solutionસ્થિર સ્થિતિમાં રહેલા પદાર્થ પાસે શું હશે ?
