In simple harmonic motion, starting from rest,
At \(t=0, x=A\)
\(x= Acos\omega t\) \(...(i)\)
\( When\,\,\, t=\tau, x=A-a\)
When \(t=2 \tau, x=A-3 a\)
From equation \(( i )\)
\(A-a=A \cos \omega \tau\) \(...(ii)\)
\(A-3 a=A \cos 2 \omega \tau\) \(...(iii)\)
As \(\cos 2 \omega \tau=2 \cos ^{2} \omega \tau-1 \ldots(\mathrm{iv})\)
From equation \((ii),\) \((iii)\) and \((iv)\)
\(\frac{A-3 a}{A}=2\left(\frac{A-a}{A}\right)^{2}-1\)
\(\Rightarrow \quad \frac{A-3 a}{A}=\frac{2 A^{2}+2 a^{2}-4 A a-A^{2}}{A^{2}}\)
\(\Rightarrow A^{2}-3 a A=A^{2}+2 a^{2}-4 A a\)
\(\Rightarrow \quad 2 a^{2}=a A \Rightarrow \quad A=2 a\)
\(\Rightarrow \quad \frac{a}{A}=\frac{1}{2}\)
Now, \(A-a=A \cos \omega \tau\)
\(\Rightarrow \quad \cos \omega \tau=\frac{A-a}{A} \Rightarrow \quad \cos \omega \tau=\frac{1}{2}\)
or, \(\quad \frac{2 \pi}{T} \tau=\frac{\pi}{3} \Rightarrow \quad \mathrm{T}=6 \tau\)
Download our appand get started for free
Similar Questions
- 1$1 \,m $ લંબાઈવાળું એક સાદુ લોલક $10 \,rad/s$ કોણીય આવૃત્તિથી દોલન કરે છે. લોલકનો આધાર $1 \,rad/s$ જેટલી નાની કોણીય આવૃત્તિ અને $10^{-2}\, m$ જેટલા કંપવિસ્તારથી ઉપર નીચે દોલન કરવાનું શરૂ કરે છે. લોલકની કોણીય આવૃત્તિમાં થતા સાપેક્ષ ફેરફારને _______ દ્વારા સચોટ રીતે દર્શાવી શકાયView Solution
- 2$v$ ઝડપ અને $a$ પ્રવેગથી સરળ આવર્ત ગતિ કરતાં કણ માટે નીચેનામાંથી કયું વિધાન સાચું છે?View Solution
- 3$1 \,kg$ દળ સ્પ્રિંગ પર લટકાવીને $12\, cm$ કંપવિસ્તારના દોલનો કરવવામાં આવે છે. $2\, minutes$ પછી તેનો કંપવિસ્તાર $6\, cm$ થાય છે. તો આ ગતિ માટે અવમંદનનો અચળાંક કેટલો હશે? ($In 2=0.693$ )View Solution
- 4$4\,kg$ દળ ધરાવતા કણની $x$-અક્ષની દિશામાં થતી ગતિ દરમિયાન સ્થિતિઊર્જા નીયે મુજબ આપી શકાય છે. $U=4(1-\cos 4 x)\,J$. નાના દોલની $(\sin \theta \approx \theta)$ માટે કણનો આવર્તકાળ $\left(\frac{\pi}{ K }\right) s$ છે. $K$ નું મુલ્ય $..........$ હશે.View Solution
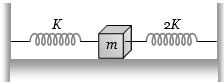
- 5આપેલ તંત્ર માટે $m$ દળના પદાર્થની આવૃત્તિ કેટલી થાય?View Solution
- 6$121\,cm$ અને $100\,cm$ લંબાઈ ધરાવતા બે લોલકો સમાન કળામાં દોલનો કરવાનું શરૂ કરે છે. કોઈક ક્ષણે, તેઓ સમાન કળામાં, તેઓના મધ્યસ્થાને છે. આ બંને ફરીવાર સમાન કળામાં તેમનાં સરેેાશ સ્થાન (મધ્ય સ્થાને) હોય તે માટે ટૂંકા લોલક દ્વારા જરૂરી લઘુત્તમ સંખ્યાના દોલનોની સંખ્યા $.....$હશે.View Solution
- 7સરળ આવર્ત ગતિ કરતાં એક બિંદુનો આવર્તકાળ $T$ છે અને ગતિનું સમીકરણ $x = a \sin (\omega t +\pi / 6)$ વડે આપવામાં આવે છે. આવર્તકાળના કેટલામાં ભાગ પછી બિંદુનો વેગ તેના મહત્તમ વેગથી અડધો થાય?View Solution
- 8એક સમક્ષિતિજ સ્પ્રિંગ સાથે જોડેલ $M$ દળનો પદાર્થ $A _{1}$ જેટલા કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે. જ્યારે $M$ દળનો પદાર્થ મધ્યમાન સ્થાન પરથી પસાર થાય છે. ત્યારે તેના પર $m$ દળનો નાનો પદાર્થ મૂકવામાં આવે છે અને બંને પદાર્થો $A_{2}$ જેટલા કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે, તો $\frac{A_{1}}{A_{2}}$ કેટલો થાય?View Solution
- 9$10\, N$ ના બળ દ્વારા એક સ્પ્રિંગને $5\, cm$ જેટલી ખેંચવામાં આવે છે. જ્યારે $2\, kg$ નું દળ લટકાવવામાં આવે તો દોલનોનો આવર્તકાળ $.....\,s$ છે.View Solution
- 10View Solutionપ્રણોદિત દોલનોના કિસ્સામાં, સરળ આવર્ત ગતિ કરતાં કણની આવૃત્તિ
