એક કણ સ્થિર સ્થિતિમાંથી અચળ પ્રવેગથી $(p - 1) sec$ માં $s_1$ અંતર અને $p\; sec$ માં ${S_2}$ અંતર કાપતો હોય,તો ${({p^2} - p + 1)^{th}} sec$ માં કેટલું સ્થાનાંતર કરે?
Diffcult
Download our app for free and get started
a
(a) From \(S = ut + \frac{1}{2}a\;{t^2}\)
(a) From \(S = ut + \frac{1}{2}a\;{t^2}\)
\({S_1} = \frac{1}{2}a{(P - 1)^2}\) and \({S_2} = \frac{1}{2}a\;{P^2}\) \([As\;u = 0\)]
From \({S_n} = u + \frac{a}{2}(2n - 1)\)
\({S_{{{({P^2} - P + 1)}^{th}}}} = \frac{a}{2}\left[ {2({P^2} - P + 1) - 1} \right]\)
\( = \frac{a}{2}\left[ {2{P^2} - 2P + 1} \right]\)
It is clear that \({S_{{{({P^2} - P + 1)}^{th}}}} = {S_1} + {S_2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પદાર્થને અમુક ઉંચાઇથી મુકત કરતાં તે $5 \,sec$ એ જમીન પર આવે છે.જો પદાર્થની $3\, sec$ એ સ્થિર કરી દેવામાં આવે અને ફરીથી મુકત કરવામાં આવે તો વધેલું અંતર કાપતાં કેટલા ...........$sec$ નો સમય લાગશે?View Solution
- 2એક બલૂન $29 \,ms^{-1}$ ના વેગથી ઉપર તરફ ગતિ કરે છે.તેમાંથી પથ્થર મૂકતાં તે $10 \,sec$ માં જમીન તે આવે છે તો બલૂન કેટલી ઊંચાઈએ ($m$ માં) હશે ત્યારે પથ્થર મુક્ત કરવામાં આવ્યો હશે?View Solution
($g = 9.8\,m/{s^2}$)
- 3એક પેરશુટિસ્ટ કૂદીને $50\, m$ અંતર સુધી ઘર્ષણ વગર પતન કરે છે. જ્યારે તે પેરશૂટ ખોલે છે ત્યારથી $2\, m/s^2$ ની પ્રતિપ્રવેગી ચાલુ કરે છે. તે $3\, m/s$ ની ઝડપથી જમીન પર પહોચે છે. તો તે $........... m$ ઊંચાઈ એ થી કૂદયો હશે.View Solution
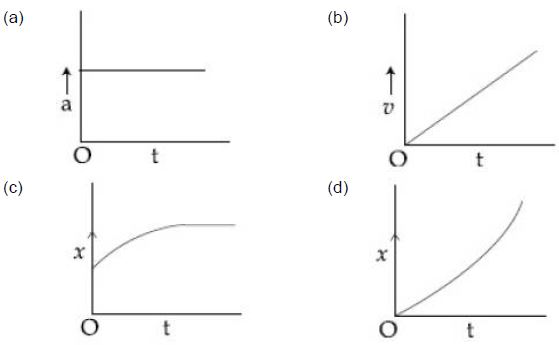
- 4એક કણ ઉદગમ સ્થાન $O$ પર સ્થિર સ્થિતિમાંથી શરૂ કરીને ધન $x -$ અક્ષ પર નિયમિત પ્રવેગી ગતિ કરે છે.આ ગતિ ને ગુણાત્મક રીતે રજૂ કરતી તમામ આકૃતિઓ ઓળખો.View Solution
($a =$ પ્રવેગ , $v =$ વેગ , $x =$ સ્થાનાંતર , $t =$ સમય)
- 5બે કાર $A$ અને $B$ શરૂઆતમાં સ્થિર છે. જો કાર $A$ $40\, m/sec$ ના અચળ વેગથી અને $B$ સમાન દિશામાં $4\,m/{s^2}$ ના પ્રવેગથી ગતિની શરૂઆત કરે તો કાર $B $ કાર $A$ ને કેટલા સમય($sec$ માં) પછી પકડી શકે?View Solution
- 6એક ઢોળાવ વાળા સમતલ પર એક નાનકડો બ્લોક ઘર્ષણ રહિત ગતિ કરે છે. ધારો કે ${S_n}$ એ $t = n - 1$ to $t = n$ સમય માં કાપેલું અંતર છે તો $\frac{{{S_n}}}{{{S_{n + 1}}}}$ શું થાય?View Solution
- 7એક કણ તેના કુલ અંતરનો અડધું અંતર $v_{1}$ ઝડપે અને બીજું અડધું અંતર $v_{2}$ ઝડપે કાપે છે. સમગ્ર મુસાફરી દરમિયાન તેની સરેરાશ ઝડપ કેટલી હશે?View Solution
- 8એક બોલને શિરોલંબ ઉપર તરફ ફેંકવામાં આવે છે. જ્યારે તે તેની મહત્તમ ઊંચાઈના અડધા ભાગ સુધી પહોંચે, ત્યારે તેનો વેગ $10 \;m/s$ છે. બોલ કેટલી ઊંચાઈ ($m$ માં) સુધી જશે? ($g = 10\; m/s^2$ લો)View Solution
- 9A body falling under gravity covers two points $\mathrm{A}$ and $\mathrm{B}$ separated by $80 \mathrm{~m}$ in $2 \mathrm{~s}$. The distance of upper point A from the starting point is $\mathrm{m}$ (use $\mathrm{g}=10 \mathrm{~ms}^{-2}$ ).View Solution
- 10View Solutionનીચેનાં બધાં જ આલેખો એક સમાન ગતિને રજૂ કરે છે. તેમાંનો કોઇ એક તેને ખોટી રીતે રજૂ કરે છે. તે શોધો.