એક મોલ એક પરમાણ્વિક આદર્શ વાયુ માટે $PV$ ગ્રાફ આપેલ છે. $BC$ પથ પર વાયુ દ્વારા પ્રાપ્ત થતું મહત્તમ તાપમાન કેટલું હશે?
AIIMS 2011, Easy
Download our app for free and get started
a
Equation of the \(BC\)
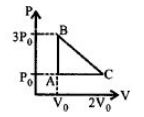
Equation of the \(BC\)
\(p = {p_0} - \frac{{2{P_0}}}{{{V_0}}}\left( {V - 2{V_0}} \right)\)
using=\(PV=nRT\)
Temperature,\(T = \frac{{{P_0}V - \frac{{2{P_0}{V^2}}}{{{V_0}}} + 4{P_0}V}}{{1 \times R}}\)
\(\left( {n = 1\,mole\,given} \right)\)
\(T = \frac{{{P_0}}}{R}\left[ {5V - \frac{{2{V^2}}}{{{V_0}}}} \right]\)
\(\frac{{dT}}{{dV}} = 0 \Rightarrow 5 - \frac{{4V}}{{{V_0}}} = 0 \Rightarrow V = \frac{5}{4}{V_0}\)
\(T = \frac{{{P_0}}}{R}\left[ {5 \times \frac{{5{V_0}}}{4} - \frac{2}{{{V_0}}} \times \frac{{25}}{{16}}V_0^2} \right] = \frac{{25}}{8}\frac{{{P_0}{V_0}.}}{R}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઅચળ તાપમાન પર એેક વાયુ ફેરફારમાંથી પસાર થાય છે. નીચેનામાંથી કઈ રાશિ સ્થિર (નિશ્ચિત) જળવાઈ રહે છે ?
- 2$ {27^o}C $ તાપમાને અને $8$ વાતાવરણ દબાણે ટાયરની ટયુબમાં હવા ભરેલ છે.ટયુબ ફાટતાં હવાનું તાપમાન કેટલું થશે? [હવા માટે $\,\gamma = \,1.5$]View Solution
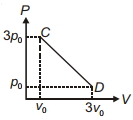
- 3પ્રક્રિયા $C D$ એ આકૃતિમાં દર્શાવેલ છે, જ્યારે તંત્રને $C$ થી $D$ સુધી લઈ જવામાં આવે ત્યારે, તંત્રના તાપમાન સાથે શું થાય છે?View Solution
- 4કાર્નોટ એન્જિન $127\,^oC$ તાપમાનવાળા ઉષ્મા પ્રાપ્તિ સ્થાનમાથી $1000\,J$ ઉષ્માનું શોષણ કરીને ઠારણ વ્યવસ્થામાં $600\,J$ ઉષ્મા ગુમાવે છે.એન્જિનની કાર્યક્ષમતા અને ઠારણ વ્યવસ્થાનું તાપમાન કેટલું કેટલું હશે?View Solution
- 5$P (V-b)=RT$ સ્થિતિ સમીકરણનું પાલન કરતા એક મોલ વાયુને $(P_1-V_1)$ અવસ્થામાંથી $(P_2-V_2)$ અવસ્થામાં એવી રીતે વિસ્તારિત કરવામાં આવે છે કે જેથી $P-V$ આલેખ સીધી રેખા મળે છે. તો કાર્ય શેના વડે આપવામાં આવે છે?View Solution
- 6પાણીના ઉત્કલનબિંદુ અને ઠારણબિંદુ વચ્યે કાર્યરત એન્જિનનીView Solution
$1$. કાર્યક્ષમતા $27 \%$ થતી વધારે હોય.
$2$. કાર્યક્ષમતા આ જ બે તાપમાનો વચ્ચે કાર્યરત કાર્નોટ એન્જિની કાર્યક્ષમતા કરતા ઓછી હોય.
$3$. કાર્યક્ષમતા $27 \%$ જેટલી હોય.
$4$. કાર્યક્ષમતા $27 \%$ કરતા ઓછી હોય.
નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
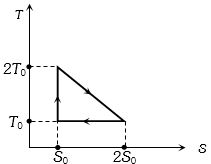
- 7View Solutionપ્રતિવર્તી એન્જિન ચક્રનો તાપમાન એન્ટ્રોપી આલેખ નીચે આપેલ છે તો તેની કાર્યક્ષમતા કેટલી થાય?
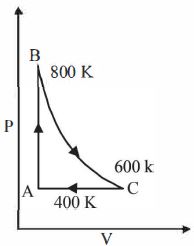
- 8આકૃતિમાં બતાવ્યા પ્રમાણે એક મોલ દ્વિ પરમાણ્વિક આદર્શ વાયુ ચક્રીય-પ્રક્રિયા $ABC$ માંથી પસાર થાય છે.પ્રક્રિયા $BC$ એ સમોષ્મી છે. $A,B$ અને $C$ આગળ તાપમાન અનુક્રમે $400 $ $K$,$800$ $K$ અને $600$ $K$ છે.નીચે આપેલ વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.View Solution
- 9$\gamma=1.5$ ધરાવતા વાયુની સમોષ્મી પ્રક્રિયા કરીને તેનું કદ $1200\, {cm}^{3}$ થી $300\, {cm}^{3}$ સુધી સંકોચવામાં આવે છે. જો શરૂઆતનું દબાણ $200\, {kPa}$છે . આ પ્રક્રિયામાં વાયુ દ્વારા થતું કાર્ય ($J$ માં) કેટલું હશે?View Solution
- 10એક સાયકલના ટાયરમાં $27^{\circ}\,C$ તાપમાને હવાનું દબાણ $270\,KPa$ છે. જ્યારે તાપમાન વધીને $36^{\circ}\,C$ થાય, ત્યારે તેના ટાયરમાં હવાનું અંદાજિત દબાણ $.........\,KPa$ થશે.View Solution