Here,
Speed of the automobile,
\(v = 54\,km\,{h^{ - 1}} = 54 \times \frac{5}{{18}}\,m\,{s^{ - 1}} = 15\,m\,{s^{ - 1}}\)
Radius of the wheel of the automoblie, \(R = 0.45 m\)
Moment of inertia of the wheel about its axis of rotation, \(I = 3 \,kg\) \({m^2}\)
Time in which the vehicle brought to rest. \(t = 15\, s\)
The initial angular speed of the wheel is
\(\omega i = \frac{v}{R} = \frac{{15\,m\,{s^{ - 1}}}}{{0.45\,m}} = \frac{{1500}}{{45}}rad\,{s^{ - 1}} = \frac{{100}}{3}rad\,{s^{ - 1}}\)
and its final angular speed is
\({\omega _f} = 0\) (as the vehicle comes to rest)
\(\therefore \) The angular retardation of the wheel is
\(\alpha = \frac{{{\omega _f} - {\omega _i}}}{t} = \frac{{0 - \frac{{100}}{3}}}{{15\,s}} = - \frac{{100}}{{45}}\,rad\,{s^{ - 2}}\)
The magnitude of required torque is
\(\tau = I\left| \alpha \right| = \left( {3\,kg\,{m^2}} \right)\left( {\frac{{100}}{{45}}rad\,{s^{ - 2}}} \right)\)
\( = \frac{{20}}{3}\,kg\,{m^2}{s^{ - 2}} = 6.66\,kg\,{m^2}{s^{ - 2}}\)
Download our appand get started for free
Similar Questions
- 1View Solutionકોઈ પદાર્થના જડત્વની ચાકમાત્રા શેના ઉપર આધાર રાખે છે?
- 2View Solutionનિયમિત વર્તૂળગતિ કરતા કણની રેખીય ઝડપ ચાર ગણી કરવામાં આવે અને કોણીય વેગ બમણો કરવામાં આવે, તો કણનો કેન્દ્રગામી પ્રવેગ .....
- 3આયર્ન માંથી બે પ્લેટ $A$ અને $B$ બનાવેલ છે જેની ત્રિજ્યા અનુક્રમે $r$ અને $4r$ અને જાડાઈ અનુક્રમે $t$ અને $t/4$ છે. $A$ અને $B$ ની જડત્વની ચાકમાત્રા $I_A $ અને $I_B $ હોય તો તેમની વચ્ચેનો સંબંધ .View Solution
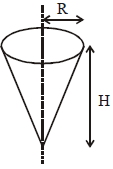
- 4આકૃતિમાં પોલો આઇસ્ક્રીમ કોન છે ,તેનું દળ $M,$ ઉપરની ત્રિજ્યા $R$ અને ઊંચાઈ $H$ છે,તો આપેલી અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા ......View Solution
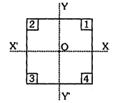
- 5આકૃતિમાં નિયમિત ચોરસ પ્લેટ દર્શાવેલી છે. જેના ખૂણા પરથી ચાર સમાન ચોરસ દૂર કરવામાં આવ્યા છે. ચોરસ $1$ અને $2$ ને દૂર કરતાં $ C.M.$ ક્યાં મળશે ?View Solution
- 6નીચે બે વિધાનો આપેલા છે : એક વિધાન $A$ અને બીજું કારણ $R$ વડે દર્શાવેલ છે.View Solution
વિધાન $A :$ $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી વર્તુળાકાર તકતી લગભગ $X, Y$ અક્ષ (તેના પ્લેનમાંથી પસાર થતી) અને $Z-$ અક્ષ જે તેના પ્લેન પર લંબ છે તેને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે $I_{x}, I_{y}$ અને ${I}_{z}$ છે. ત્રણેય અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા સમાન હશે.
Reason $R$ : ચાકગતિ કરતાં દઢ પદાર્થનું દળ અને આકાર નિશ્ચિત હોય છે.
ઉપર આપેલા વિધાનો માટે નીચેનામાંથી યોગ્ય વિકલ્પ પસંદ કરો.
- 7$0.1\ m$ ત્રિજ્યા ધરાવતા એક વર્તુળાકાર તકતી (નહિવત વજન) પર $2\ kg$ દળના $5$ કણ છે. તકતીના કેન્દ્ર માથી અને તેના સમતલને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ........ $kg\,m^2$ થાય.View Solution
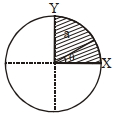
- 8આકૃતિમાં $M$ દળ અને $\sigma$ દળ ઘનતા ધરાવતી તકતી દર્શાવેલ છે. આકૃતિમાં રેખાંકિત કરેલ તકતીના ચૌથા ભાગના દ્રવ્યમાન કેન્દ્રના યામ $\frac{x}{3} \frac{a}{\pi}, \frac{x}{3} \frac{a}{\pi}$ હોય તો તો $x$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશે?$[ a=$ રેખાંકિત કરેલ ભાગનું ક્ષેત્રફળ$]$View Solution
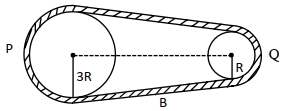
- 9આપેલ આકૃતિમાં બે પૈડાં $P$ અને $Q$ ને બેલ્ટ $B$ થી જોડવામાં આવેલ છે. $P$ પૈડાની ત્રિજયા $Q$ પૈડાં કરતાં ત્રણ ગણી છે. સમાન ચાકગતિઊર્જાના કિસ્સામાં તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર $\left(\frac{{I}_{1}}{{I}_{2}}\right)$, ${x}: 1$ હોય તો ${x}$ નું મુલ્ય કેટલું હશે?View Solution
- 10કોઈ પદાર્થ પર ટોર્ક લગાવ્યા વગર, પરંતુ જડત્વની ચાકમાત્રા માં ફેરફાર થવાથી તેની કોણીય ઝડપ ${\omega _1}$ માથી ${\omega _2}$ થાય છે. તો બંને કિસ્સામાં ચક્રાવર્તનની ત્રિજ્યાનો ગુણોત્તર શું થશે?View Solution
