એક નાનો $d l$ લંબાઈનો પ્રવાહ પસાર કરતો પદાર્થ $(1,1,0)$ પર રહેલ છે. અને ${+z}$ દિશામાં પ્રવાહ પસાર થાય છે.ઉગમબિંદુ આગળનું ચુંબકીય ક્ષેત્ર $\overrightarrow{B_1}$ અને બિંદુ $(2,2,0)$ આગળ ચુંબકીય ક્ષેત્ર $\overrightarrow{B_2}$ હોય, તો
Medium
c
(c)
(c)
\(\vec{B}=\frac{\mu_0}{4 \pi} \frac{\times \vec{r}}{r^3}\) for \(B_1 \;\;\vec{r}=(-\hat{i}-\hat{j})\)
\(\therefore \vec{B}_1=\frac{\mu_0}{4 \pi} \frac{i}{2 \sqrt{2}} \hat{k} \times(-\hat{i}-\hat{j}) \ldots .(1)\)
for \(B_2\;\; \vec{r}=\hat{i}+\hat{j}\)
\(\vec{B}_2=\frac{\mu_0}{4 \pi} \frac{i \hat{k} \times(\hat{i}+\hat{j})}{2 \sqrt{2}} \ldots \ldots(2)\)
from (1) and (2)
\(\vec{B}_t=-\vec{B}_2\) and \(\left|\vec{B}_1\right|=\left|\vec{B}_2\right|\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionજ્યારે ગજિયા ચુંબકને મેગ્નેટિક મોમેન્ટ સાથે પૃથ્વીનાં ચુંબકીય ક્ષેત્રને સમાંતર રાખીએ તો કેટલા તટસ્થ બિંદુઓ મળે
- 2View Solutionકાયમી ચુંબક માટે વપરાતું દ્રવ્ય
- 3બે સરખાં કદનાં ગજિયા ચુંબકોની મેગ્નેટિક મોમેન્ટોનો ગુણોત્તર $1: 2$ છે.જો તેમનાં ધ્રુવો સમાન રહે તે રીતે એકની ઉપર બીજો મુકીએ તો ચુંબકીય ક્ષેત્રમાં તે નાં દોલનોનો સમયગાળો $3s$ છે.જો એેકને ઉલટાવીએે તો આા ક્ષેત્ર માટે દોલન માટેનો સમયગાળોView Solution
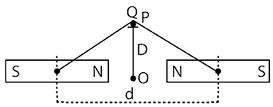
- 4બે સરખાં ગજિયા ચુંબકોને $d$ અંતરે જડેલા છે. આકૃતિમાં દર્શાવ્યા મુજબ સ્થિર વિદ્યુતભાર $Q$ ને બંને ચુંબકોનાં વચ્ચેનાં ભાગમાં $P$ બિંદુએ કેન્દ્ર $O$ થી $D$ અંતરેથી રાખવામાં આવે છે. $Q$ વિદ્યુતભાર પર લાગતું બળView Solution
- 5કોઈ અનુંચુંબકીય (પેરામેગ્નેટીક) પદાર્થમાં $10^{28}$ પરમાણુ પ્રતિ $m^3$ માં રહેલા છે. તેની $350\, K$ તાપમાને ચુંબકીય સસેપ્ટિબિલીટી $2.8\times 10^{-4}$ છે.તો તેની $300 \,K$ તાપમાને સસેપ્ટિબિલીટી કેટલી થશે?View Solution
- 6$10^{-3}\, m ^{3}$ કદ અને $1000$ સાપેક્ષ પરમિએબિલિટી ધરાવતા લોખંડના સળિયાને $10$ આટા/$cm$ ધરાવતા સોલેનોઇડ માં મૂકીને $0.5\,A$ પ્રવાહ પસાર કરતા ઉદ્ભવતી મેગ્નેટિક મોમેન્ટ $...........Am^2$View Solution
- 7એક પ્રબળ ચુંબકીય ધ્રુવની સામે એક તકતીને સમક્ષિતિજ સપાટી ઉપર મુકવામાં આવે છે.. . . . . માટે બળ જોઈશે.View Solution
$A$. જો તક્તી ચુંબકીય હશે તો તેને જકડી રાખવા
$B$. જો તક્તી અચુંબકીય હશે તો તેને જકડી, રાખવા
$C$. જો તક્તી સુવાહક હશે તો તેને નિયમિત વેગથી ધ્રુવથી દૂર તરફ ગતિ કરાવવા
$D$. જો તક્તી અવાહક અને અધ્રુવીય હશે તો તેન નિયામત વેગથી ધ્રુવથી દૂર તરફ ગતિ કરાવવા
નીચે આપેલા વિકલ્પોમાંથી સીથી યોગ્ય ઉત્તર પસંદ કરો.
- 8ચુંબકીય મેરેડિયન સાથે $30^{\circ}$ નો ખૂણો બનાવતા સમતલમાં ડીપ એન્ગલ $45^{\circ}$ નો છે. સાચો ડીપ એન્ગલ શોધો.View Solution
- 9View Solutionસમાન ધ્રુવમાન અને સમાન લંબાઇ ધરાવતા બે ચુંબકોના અસમાન ધ્રુવો ભેગા રાખીને દોલનો કરાવતાં તેનો આવર્તકાળ કેટલો થાય?
- 10View Solutionચુંબકીય પદાર્થને ગરમ કરતાં
