એક નક્કર ગોળાકાર માટે $\theta$ ખૂણો ધરાવતાં એક ઢોળાવયુક્ત સમતલ પરથી સરક્યાં વિના ગબડવા માટેનો લઘુત્તમ ઘર્ષણાંક શું હશે?
Medium
Download our app for free and get started
a
(a)
(a)
\(\mu=\frac{I \tan \theta}{I+m r^2}=\frac{\frac{2}{5} m r^2 \tan \theta}{\frac{2}{5} m r^2+m r^2}\)
\(=\frac{2 \tan \theta}{7}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએક તકતી અને એક ગોળાની ત્રિજયા સમાન પણ દ્રવ્યમાન જુદા છે તે સમાન ઊંચાઇ અને લંબાઇના બે ઢાળ પરથી ગબડે છે. બેમાંથી કયો પદાર્થ તળિયે પહેલો પહોંચશે?
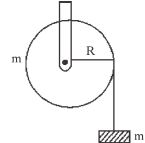
- 2$m $ દળ ધરાવતા પદાર્થને વજનરહિત દોરી વડે $m$ દળ અને $R$ ત્રિજયા ધરાવતા સમાંગી પોલા નળાકાર પર લટકાવવામાં આવે છે.જો દોરી નળાકાર પર સરકે નહિ તો તે સ્થિતિમાં આપેલ પદાર્થ કેટલા ગુરુત્વપ્રવેગથી નીચે પડશે?View Solution
- 3View Solutionએવી પરિસ્થિતિ લો કે જેમાં એક રિંગ, નક્કર નળાકાર અને નક્કર ગોળો સમતલ ઢાળ પરથી સરક્યા વિના ગબડે છે. ધારો કે તેઓ સ્થિર સ્થિમાંથી શરૂઆત કરે છે અને તેમના વ્યાસ સમાન છે.
આ પરિસ્થિતિ માટે યોગ્ય વિધાન કયું છે
- 4$L$ લંબાઇનો સળિયા બે માણસના ખંભા પર છે. છેડા પરના એક માણસ પર $ 1\over 4 $ માં ભાગનું વજનબળ લાગે છે. તો બીજો માણસ આ છેડાથી કેટલે દૂર હશે?View Solution
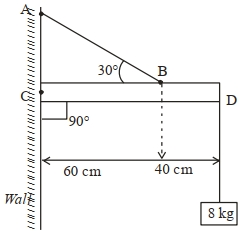
- 5એક $8\,kg$ દળ ધરાવતા પદાર્થને $2\,kg$ દળ અને $1\,m$ લંબાઈ ધરાવતા એક નિયમિત સળિયા $CD$ ના એક છેડાથી લટકાવેલ છે, સળિયાનો બીજો છેડો આકૃતિમાં દર્શાવ્યા અનુસાર ઉર્ધ્વ (શિાોલંબ) દિવાલ સાથે ટકાવેલ છ. તે સળિયાને $A B$ તાર (કેબલ) વડે અવી રીતે ટેકવેલો છે કે જથી તંત્ર સંતુલનમાં રહે. કેબલમાં તણાવ $............\,N$ હશે.(ગુરુત્વીયપ્રવેગ $g=10\,m / s ^2$ )View Solution
- 6એ કારનું પૈડું $1200\ r.p.m.$ ની ઝડપથી ફરે છે $10\ sec$ માટે પ્રવેગ આપતા તે $4500\ r.p.m. $ ની ઝડપે ફરવા લાગે તો પૈડાંનો કોણીય પ્રવેગ કેટલો થાય ?View Solution
- 7View Solutionએક તરવેયો કોઈ ઉંચાઈથી નદીમાં ફૂદકો મારતી વખતે હવામાં સરળતાથી લૂપ બનાવે છે. જો તે,
- 8View Solutionએક તકતી અને એક ગોળાની ત્રિજયા સમાન પણ દ્રવ્યમાન જુદા છે તે સમાન ઊંચાઇ અને લંબાઇના બે ઢાળ પરથી ગબડે છે. બેમાંથી કયો પદાર્થ તળિયે પહેલો પહોંચશે?
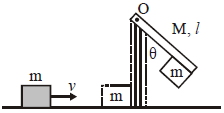
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $m =1\, kg$ દળનો એક પદાર્થ $v=6\, m / s$ જેટલા વેગથી એક ઘર્ષણરહિત સપાટી પર ગતિ કરીને એક સળિયા સાથે અથડાયને તેની સાથે જોડાય જાય છે. આ સળિયો $O$ બિંદુ સાથે જડેલ છે અને અથડામણના કારણે તે $\theta$ ખૂણો બનાવે છે. જો સળિયાનું દળ $M =2 \,kg $ અને લંબાઈ $l=1\, m $ હોય તો $\theta$ ખૂણાનું મૂલ્ય કેટલું હશે?View Solution
$(\left.g=10 \,m / s ^{2}\right)$
- 10View Solutionગુરૂત્વાકર્ષકની અસર હેઠળ શિરોલંબ રીતે અધોદિશામાં પડતો પદાર્થ બે અસમાન દળોનાં ટુકડાંઓમાં વિભાજિત થાય છે. બંને ટુકડાઓનું એક સાથે લેવામાં આવેલું દ્રવ્યમાન કેન્દ્ર શું થાય?