એક પારદર્શક નકકર નળાકારના દ્રવ્યનો વક્રીભવનાંક $\frac{2}{{\sqrt 3 }}$ છે,તેની આસપાસ હવા છે. આકૃતિમાં દર્શાવ્યા મુજબ આ નળાકારના એક છેડાના મઘ્યબિંદુ પાસે એક પ્રકાશકિરણ આપાત કરવામાં આવે છે,તો આપાતકોણના કયા મૂલ્ય માટે નળાકારમાં દાખલ થયેલ પ્રકાશકિરણ તેની દીવાલ સાથે ઘસડાઇને આગળ વધશે?
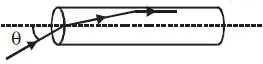

AIEEE 2009, Diffcult
d
Applying Snell's law at \(Q\)
Applying Snell's law at \(Q\)
\(n=\frac{\sin 90^{\circ}}{\sin C}=\frac{1}{\sin C}\)
\(\therefore \sin C=\frac{1}{n}=\frac{\sqrt{3}}{2}\)
\(\therefore \mathrm{C}=60^{\circ}\)
Applying Snell's Law at \(P\)
\(n=\frac{\sin \theta}{\sin (90-C)} \Rightarrow \sin \theta=n \times \sin (90-C) ;\) from \((1)\)
\(\Rightarrow \sin \theta=n \cos\)
\(\therefore \theta=\sin ^{-1}\left[\frac{2}{\sqrt{3}} \times \cos 60^{\circ}\right]\)
or \(\quad \theta=\sin ^{-1}\left(\frac{1}{\sqrt{3}}\right)\)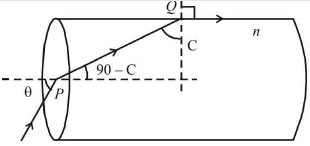
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
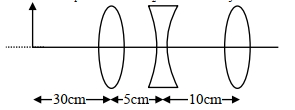
- 1લેન્સના સંયોજન વડે ૨ચાતા પ્રતિબંબનું સ્થાન. . . . . છે. $\mathrm{f}_1=10 \mathrm{~cm} \quad \mathrm{f}_2=10 \quad \mathrm{f}_3=30 \mathrm{~cm}$View Solution
- 2View Solutionએસ્ટ્રોનોમિકલ ટેલિસ્કોપનો સામાન્ય દ્રષ્ટિ માટે મેગ્નિફિકેશ પાવર સાદી રીતે ........થી આપી શકાય છે.
- 3પ્રિઝમનો પ્રિઝમકોણ $60°$ અને ન્યૂનત્તમ વિચલનકોણ $30°$ છે. ત્યારે આપાતકોણ ........$^o$ થશે.View Solution
- 4પાત્રમાં પ્રવાહી $120\,mm$ ઊંચાઇ સુધી ભરેલ છે.તેમાં રહેલ સોય $80\,mm$ ઊંડાઇ પર દેખાતી હોય,તો પ્રવાહીનો વક્રીભવનાંક કેટલો હશે?View Solution
- 5માછલી ઘરમાં પાણીની સપાટીથી $30\,cm$ ઊંડાઈએ રહેલી માછલી પાણીની સપાટી થી $50\,cm$ ઊંચાઈએ રહેલા બલ્બને જોઈ શકે છે. આ માછલી બલ્બનું પ્રતિબિંબ પણ જોઈ શકે છે. પાણીની કુલ ઊંડાઈ $60\,cm$ છે. માછલી ને દેખાતા બન્ને પ્રતિબિંબ વચ્ચેનું અંતર.View Solution
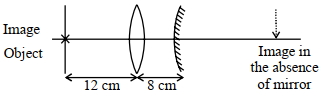
- 6એક વસ્તુને બહિર્ગોળ લેન્સથી $12 \,{cm}$ અંતરે મૂકેલો છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે $15 \,{cm}$ કેન્દ્રલંબાઈ ધરાવતા બહિર્ગોળ અરિસાને લેન્સની બીજી બાજુ $8 \,{cm}$ અંતરે મૂકેલો છે. વસ્તુનું પ્રતિબિંબ વસ્તુ પાસે જ મળે છે. જ્યારે બહિર્ગોળ અરિસાને દૂર કરવામાં આવે ત્યારે વાસ્તવિક અને ઊલટું પ્રતિબિંબ મળે છે. તો વસ્તુથી આ પ્રતિબિંબ કેટલા $(cm)$ દૂર બનશે?View Solution
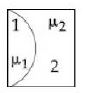
- 7$R$ ત્રિજ્યા ધરાવતા અલગ અલગ પદાર્થમાથી બનેલા સમતલ અંતર્ગોળ અને સમતલ બહિર્ગોળ લેન્સને આકૃતિમાં દર્શાવ્યા પ્રમાણે મૂકેલા છે.પહેલા લેન્સનો વક્રીભવનાંક $\mu_1$ અને બીજા લેન્સનો વક્રીભવનાંક $\mu_2$ હોયતો તંત્રની સંયુક્ત કેન્દ્રલંબાઇ કેટલી થશે?View Solution
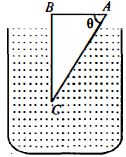
- 8$1.5$ વક્રીભવનાંક ધરાવતા પ્રિઝમને આકૃતિમાં દર્શાવ્યા પ્રમાણે પાણીમાં દુબાડેલ છે. એક પ્રકાશનું કિરણ $AB$ સપાટી પર લેમ્બ આપાત કરવામાં આવે છે જેનું પૂર્ણ આંતરિક પરાવર્તન કરીને $BC$ સપાટી પર પહોચડવા માટે $\theta$ નું મૂલ્ય કેટલું હોવું જોઈએ?View Solution
- 9એક સમાંતર પ્રકશકિરણને $30 \,cm$ જેટલો વ્યાસ અને $1.5$ જેટલો વક્રીભવનાંક ધરાવતા પારદર્શક ગોલીય ગોળા ઉપર પડવા દેવામાં આવે છે. ગોળાના કેન્દ્રથી ............ $mm$ અંતરે પ્રકાશ કિરણપૂંજ કેન્દ્રિત થશે.View Solution
- 10એક વસ્તુને પડદાથી $1.50\, m$ અંતરે મૂકેલ છે અને બહિર્ગોળ અરીસાને વચ્ચે મૂકવામાં આવતાં પડદા પર ચાર ગણું મોટું પ્રતિબિંબ ઉદ્દભવે છે. તો લેન્સની કેન્દ્રલંબાઈ .....$cm$ હશે.View Solution
