એક પારંભિક સ્થિર યંત્ર એક ઘર્ધણઘર્ષણમુક્ત સપાટી પર પડ્યું છે. તે $2$ ટુકડાઓમાં ફાટે છે અને તે સપાટી પર ખસે છે. જો એક ટુકડો ધન $x$ દિશામાં ગતિ કરી રહ્યો હોય તો બીજો ટુક્ડો કઈ દિશામાં ગતિ કરશે ?
Easy
Download our app for free and get started
c
(c)
(c)
Since first part is moving positive \(x\)
\(\therefore\) Second part will confirm move in negative.
\(\therefore\) Option \(C\) is correct.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
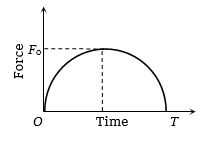
- 1સ્થિર સ્થિતિમાં રહેલા $m$ દળના કણ પર લાગતા બળનો આલેખ આપેલ છે.બળ બંધ થયા પછી તેનો વેગ $u$ હોય તો $u$ કેટલો થાય?View Solution
- 2એક $Mg$ વજનને એક દોરીનાં મધ્યમાં લટકાવવામાં આવ્યું છે જેના છેડાઓ સમાન સ્તર પર છે. દોરી હવે સમક્ષિતિજ નથી. દોરીને સંપૂર્ણપણે સીધી કરવાં માટે જરરી લઘુત્તમ તણાવ બળ છે.View Solution
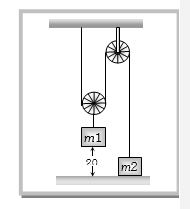
- 3જો $ m_1 = 4m_2$ હોય,તો $m_2 $ નો પ્રવેગ કેટલો થાય? $m_1 $ નો પ્રવેગ $a$ છે.View Solution
- 4લિફ્ટમાં સ્પ્રિંગ બેલેન્સ પર $2\, kg$ નો દળ લટકાવેલ છે. હવે લિફ્ટ $2 \,m/sec^2$ ના પ્રવેગથી ઉપર તરફ ગતિ કરે, તો સ્પ્રિંગ બેલેન્સનું અવલોકન ....... $kg$ હશે.View Solution
- 5$4 \,{kg}$ દળવાળી બંદૂકમાંથી $4\,g$ દળવાળી ગોળી છોડવામાં આવે છે. જો ગોળી $50\, {ms}^{-1}$ ની ઝડપ સાથે આગળ વધે છે, તો બંદૂકને આપવામાં આવતો આઘાત અને બંદૂકના પાછળના ભાગનો વેગ કેટલો હશે?View Solution
- 6એક તારના ટુકડાને $Y = Kx^2$ અનુસાર પરવલય આકારમાં વાળવામાં આવેલ છે. તેની અંદર $m$ દળનું એક જંતુ છે, જે તાર પર ઘર્ષણરહિત સરકી શકે છે. જ્યારે તાર સ્થિર હોય ત્યારે તે પરવલયના સૌથી નીચેના બિંદુ પાસે છે. હવે તારને $ X-$ અક્ષને સમાંતર વલય જેટલા અચળ પ્રવેહથી ગતિ કરાવવામાં આવે છે, તો હવે જંતુ તારની સાપેક્ષે સ્થિર રહી શકે તેવું નવા સંતુલિત સ્થાનનું $ Y-$ અક્ષથી અંતર કેટલું હશે ?View Solution
- 7$m$ દળનું કાચલું $v$ વેગથી ગતિ કરી રહ્યું છે અને અચાનક બે ભાગ માં તૂટી જાય છે. $m/3$ દળ ધરાવતો ભાગ સ્થિર રહે છે. તો બીજા ભાગનો વેગ કેટલો હશે?View Solution
- 8View Solutionજો કોઈ તંત્રનો અંતિમ વેગમાન એ તેના પ્રારંભિક વેગમાનને બરાબર હોય તો
- 9$M$ દળ અને $L$ લંબાઈની એકરૂપ દોરીને તેનાં ઉપરનાં સંતિમ છેડાને દઢ આધાર સાથે શિરોલંબ રીતે જોડેલ છે. તો પછી દઢ આધારથી $l$ અંતર પર દોરીમાં ઉદભવતો તણાવ શોધો.View Solution
- 10એક પદાર્થ $\vec F = 6\hat i - 8\hat j + 10\hat k$ બળની અસર હેઠળ $1\ m/s^2$ જેટલો પ્રવેગ પ્રાપ્ત કરે છે. આ પદાર્થનું દળ કેટલું હશે?View Solution